Considere o plano em que passa pela origem de equação cartesiana
e a transformação linear espelhamento (ou reflexão) em relação ao plano Denote por a matriz de E na base canônica.
(a) Considere a base ortonormal de
e o vetor (escrito na base canônica). Determine a segunda coordenada de v na base
(b) Escreva na forma , onde Q é uma matriz ortogonal e D é diagonal.
(c) Determine explicitamente a matriz
Passo 1
(a) Vamos dizer que:
Para escrever v na base , fazemos:
Queremos achar b, a segunda coordenada de v na base .
Para isso, vamos tirar o produto interno com dos dois lados dessa igualdade:
Pela linearidade do produto interno:
Mas a base é ortonormal, então:
Logo:
Passo 2
(b) Lembra que quando escrevemos na forma , a matriz D é a matriz diagonal com autovalores na diagonal principal e a matriz Q é uma matriz ortogonal com autovetores ortonormais nas colunas.
A matriz é uma matriz de reflexão em torno do plano de equação .
A direção normal a esse plano é gerada pelo vetor
Se a gente considera a base ortonormal de dada no item (a):
Temos que é ortogonal ao plano , então:
Ou seja, é autovetor associado a
Porém e não são ortogonais a , mas são vetores de (reparem que os dois satisfazem a equação de ).
Por isso:
Ou seja, e são autovetores associados a .
Logo a representação diagonal é:
E:
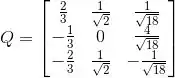
Passo 3
(c) Vamos começar calculando e separado.
Temos:
Mas:
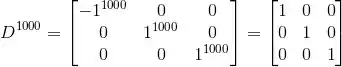
Ou seja:
De maneira análoga:
Então:
Resposta
(a)
(b) 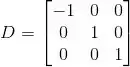
(c)