P3 de Física 1 da UFRJ - 2019.1

Um carro faz uma curva plana horizontal com velocidade de módulo constante v. Considere as afirmativas:

I A força de atrito é a força de reação à força centrípeta.

II. A aceleração do carro na curva é nula em módulo.

III. Quanto maior o raio da curva maior deve ser o módulo da força de atrito sobre o carro para que ele descreva essa curva com velocidade de módulo v.

Quais afirmativas são verdadeiras:

a) Nenhuma.

b) Apenas I

c) Apenas II

d) Apenas III

e) Apenas I e II

f) Apenas I e III

g) Apenas II e III

h) Todas

Considere as seguintes afirmações:

I. Um corpo sob a ação de uma força , se move sempre na direção e sentido desta força.

II. No movimento retilíneo uniformemente variado a aceleração tem sempre o mesmo sentido da velocidade.

III. O vetor posição de um corpo num instante t qualquer é dado por, , onde é o vetor posição inicial, é o vetor velocidade inicial e o vetor aceleração onde todos são vetores constantes em módulo direção e sentido, neste caso a trajetória do corpo é necessariamente parabólica.

Das afirmativas acima quais (ou qual) estão incorretas:

a) Todas as afirmativas.

b) Apenas I

c) Apenas II

d) Apenas III

e) Apenas I e II

f) Apenas I e III

g) Apenas II e III

h) Nenhuma das afirmativas.

Duas partículas de mesma massa se movem sobre uma reta com velocidades constantes, de mesmo módulo e sentidos contrários. Sobre esse sistema são feitas as seguintes afirmações:

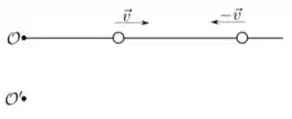
I. O momento angular de ambas as partículas com relação ao ponto é nulo

II. O momento angular de ambas as partículas com relação ao ponto é nulo

III. O momento angular total do sistema com relação aos pontos e é nulo

As afirmativas corretas são:

a) Todas as afirmativas.

b) Apenas I

c) Apenas II

d) Apenas III

e) Apenas I e II

f) Apenas I e III

g) Apenas II e III

h) Nenhuma das afirmativas.

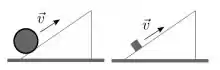
Um bloco e um cilindro são lançados, de mesma massa M, com a mesma velocidade escalar v, ao longo de planos que tem a mesma inclinação (diferente de zero), em relação à horizontal. No plano onde está o bloco não há atrito e no plano onde se encontra o cilindro há atrito suficiente para que ele role sem deslizar. Sabendo que o momento de inércia do cilindro relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é. A relação entre a altura máxima que o bloco atinge Hb e a altura máxima que o cilindro atinge HC nos respectivos planos é dada por:

a) , pois tanto a energia mecânica do bloco como a do cilindro se conserva.

b) Hb = Hc, pois tanto a energia cinética do bloco como a do cilindro se conserva.

c) Hb = Hc, pois tanto a energia mecânica do bloco como a do cilindro se conserva.

d) , pois o bloco desliza sem atrito.

e) , pois o momento angular do cilindro se conserva.

f) Não há como afirmar tal relação sem conhecermos o ângulo θ que os planos fazem com a horizontal.

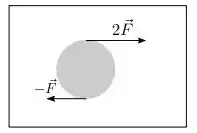
g) , pois tanto a energia mecânica do bloco como a do cilindro se conserva.

Um disco homogêneo de massa M e raio R encontra-se sobre uma mesa horizontal completamente lisa, sem estar preso a ela. Em um dado instante duas forças estão aplicadas tangencialmente na beirada do disco, uma em um ponto diametralmente oposto ao ponto de aplição da outra. Sabendo que o momento de inércia do disco relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é , e denotando por acm e α os módulos respectivos da aceleração do centro de massa do disco e da aceleração angular de rotação em torno do eixo no instante considerado, podemos dizer que:

a)

b)

c)

d)

e)

f)

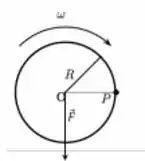
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal, de comprimento L, que faz um ângulo θ com a vertical, de modo que a partícula execute um movimento circular uniforme, com centro no ponto C, com velocidade angular ω como ilustra a figura. Sendo o módulo do torque da partícula em relação ao ponto C e a o módulo da aceleração da partícula respectivamente, podemos afirmar:

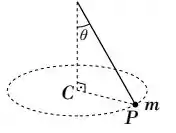
a)

b)

c)

d)

e)

f)

g)

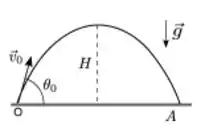
Um projétil de massa é lançado de um ponto O de um plano horizontal com velocidade de módulo e ângulo de lançamento, onde . O projétil atinge uma altura máxima H e um alcance A. Se é o módulo do momento angular do projétil ao atingir a altura máxima H e , o módulo do momento angular quando ele atinge o alcance A, ambos calculados em relação a O, então

6. Nenhuma das alternativas

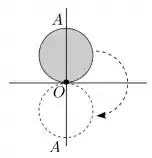
Um disco de raio R e de massa M uniformemente distribuída, possui um pequeno furo na sua periferia. Por este furo o disco é colocado no pino O, preso a uma parede vertical. No posicionamento inicial do disco o ponto A de sua periferia localizado diametralmente oposto a O está sobre o eixo vertical, acima de O; conforme mostra a figura abaixo. Como o disco está sob a condição de equilíbrio instável, ele cai girando em torno do pino O. Sabe-se que o momento de inércia deste disco em torno de um eixo que passa pelo centro de massa e perpendicular e ele é igual . Desprezando-se o atrito entre o pino e o disco, quando o ponto A passa pela linha vertical, abaixo de O, a velocidade angular ω do disco, é igual a:

Considere uma esfera que rola sem deslizar sobre uma calha simétrica que tem dois trechos retilíneos, I e II, como mostra a figura. Ela oscila descendo e subindo nos dois ramos da calha. No trecho I a força de atrito é e no trecho II, é . Considere que as únicas forças que atuam sobre a esfera sejam a força normal e a força de atrito exercidas pela calha, e o seu peso.

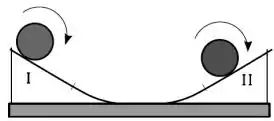
Dentre os diagramas seguintes:

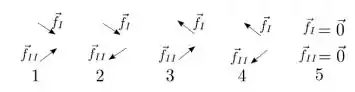
o que melhor representa o sentido e a direção das forças de atrito e nos trechos I e II é:

1. 3
2. 1
3. 2
4. 4
5. 5
6. Nenhuma das alternativas

Um arame quadrado de lado , fino, rígido e de massa desprezível, tem nos seus vértices quatro massas iguais a m. Os momentos de inércia , relativos aos respectivos eixos A, B e C mostrados na figura relacionam-se como:

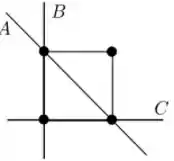
a)

b)

c)

d)

e)

f)

Um homem de massa M/5 está em pé sobre uma das extremidades de uma prancha que repousa sobre a superfície de uma lago congelado. A massa da prancha, que é distribuída de maneira uniforme em seu comprimento L, é M. O homem começa a andar em direção à outra extremidade da prancha. Desprezando o atrito entre o gelo e a prancha, determine a distância D que a prancha percorre ao fim do percurso do homem de uma extremidade à outra da prancha.

a)

b)

c)

d)

e)

f)

Uma barra é constituída de dois materiais homogêneos, aço (parte clara da barra na figura) com massa 2M e madeira (parte escura da barra) com massa M, distribuídos em cada metade da barra. Ela repousa sobre uma mesa horizontal e sem atrito. Aplica-se a mesma força , perpendicularmente ao extremo da barra nas situações (A) e (B) como indica a figura, fazendo-a girar em torno de um pino de articulação na situação (A) e na situação (B). As relações entre os módulos dos torques , em relação a , devido à força e os módulos das acelerações angulares resultantes α, nas situações (A) e (B), são dadas:

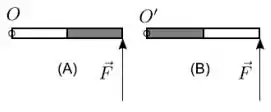
1. e .
2. e .
3. e.
4. e .
5. e .
6. Nenhuma das alternativas.

Duas partículas com velocidades iniciais perpendiculares (figura) colidem de forma totalmente inelástica. Seja p o momento linear total do sistema composto pelas duas partículas (|p|, seu módulo) e K a energia cinética total deste sistema. Comparando os valores de p e K antes e depois da colisão, pode-se afirmar que:

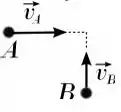
a) p é conservado, K é reduzido, porém não a zero;

b) p é conservado, K é conservado;

c) |p| é reduzido a zero, K é reduzido a zero;

d) p é conservado, K é reduzido a zero;

e) |p| é reduzido, porém não a zero, K é reduzido, porém não a zero;

f) |p| é aumentado, K é conservado;

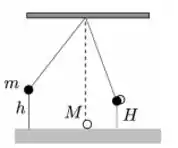
Uma massa m é pendurada por um fio ideal. Ela é abandonada da altura h a partir do repouso e colide com a massa M, também em repouso, de forma totalmente inelástica; vide a figura. Após a colisão a razão entre h e altura máxima H que ambas atingem é:

A figura abaixo representa um disco de massa M homogêneo e uniforme, de espessura desprezível, e raio R. O disco gira no sentido horário em torno do seu eixo de simetria, com velocidade angular constante de módulo ω, e move-se sob a ação da força F mantendo-se sempre num mesmo plano. Sabendo-se que a aceleração do centro de massa do disco é devida apenas a ação da força F, o módulo da aceleração do ponto P localizado na borda do disco, mostrado na figura, é: