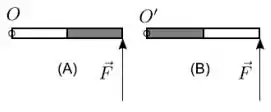
Uma barra é constituída de dois materiais homogêneos, aço (parte clara da barra na figura) com massa 2M e madeira (parte escura da barra) com massa M, distribuídos em cada metade da barra. Ela repousa sobre uma mesa horizontal e sem atrito. Aplica-se a mesma força , perpendicularmente ao extremo da barra nas situações (A) e (B) como indica a figura, fazendo-a girar em torno de um pino de articulação na situação (A) e na situação (B). As relações entre os módulos dos torques , em relação a , devido à força e os módulos das acelerações angulares resultantes α, nas situações (A) e (B), são dadas:
- e .
- e .
- e.
- e .
- e .
- Nenhuma das alternativas.
Passo 1
Bom, como a gente sabe, o torque é dado por:
Temos uma força de mesmo valor sendo aplicado numa mesma distância tanto no caso A quanto no caso B, então nosso Torque será igual nos dois casos, mas pensa comigo, a barra é comporta por dois materiais de massas diferentes, então seu centro de massa estará mais deslocado pra o lado do material mais pesado, que no caso, é o aço, a parte mais clara da barra!

Então como o centro de massa em B tá mais deslocado pra o local da força aplicada devido a diferença da distância dos seus centros de massa, e, consequentemente, do seu , então a aceleração angular de A será maior que a de B, sacou? Show!
Resposta
- e .