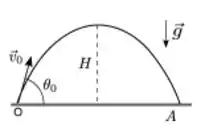
Um projétil de massa é lançado de um ponto O de um plano horizontal com velocidade de módulo e ângulo de lançamento, onde . O projétil atinge uma altura máxima H e um alcance A. Se é o módulo do momento angular do projétil ao atingir a altura máxima H e , o módulo do momento angular quando ele atinge o alcance A, ambos calculados em relação a O, então
- Nenhuma das alternativas
Passo 1
Bom, vamos começar decompondo a nossa velocidade inicial .
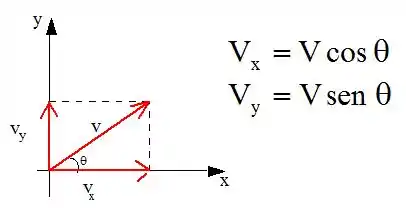
E assim como a gente viu lá em MRUV, é constante, pois não temos a presença de nenhuma aceleração nesse sentido, o que não acontece com , tendo a presença da gravidade.
Agora vamos definir os dois pontos que nós queremos. O primeiro ponto é o ponto de altura máxima, no topo da parábola da gente ali. Nesse ponto, tendo como referencial o ponto O, o vetor posição pra esse ponto é:
E o vetor velocidade nesse ponto, como na altura máxima a velocidade em y é nula, é dado por:
Lembrando agora da equação do momento angular, sabemos que:
Então vamos primeiro calcular aquele produto vetorial ali:
Show, então, temos que:
Como se pede o módulo de e esse vetor só tem uma componente, seu módulo é exatamente o módulo dessa componente, ou seja:
Como vimos lá em cima, , logo:
Beleza!
Passo 2
Da mesma forma, vamos calcular . Nesse caso, lembrando que a velocidade vertical inverte de sentido a partir da altura máxima, temos que:
Então:
Resolvendo novamente o produto vetorial acima, temos:
Então, substituindo lá em cima, ficamos com:
Calculando o módulo do momento da mesma forma que fizemos no passo 1, temos:
Pronto, o que nos dá como resposta a alternativa a).