Física 1 UFRJ 3ºEE 2019.1
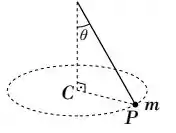
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal, de comprimento L, que faz um ângulo θ com a vertical, de modo que a partícula execute um movimento circular uniforme, com centro no ponto C, com velocidade angular ω como ilustra a figura. Sendo o módulo do torque da partícula em relação ao ponto C e a o módulo da aceleração da partícula respectivamente, podemos afirmar:
a)
b)
c)
d)
e)
f)
g)
Passo 1
Como a aceleração resultante é apenas a celeração centrípeta, basta calcularmos ela!
Show, mas quem é R? Usando decomposição de vetores, sabemos que se temos o ângulo ali em cima, o raio da circunferência vai ser dado por , então a aceleração fica:
Show, já foi uma parte!
Passo 2
E o nosso torque, como sabemos, pode ser calculado assim:
Mas notem que as forças que temos são: A tração, no fio, e a força peso.
O torque em relação ao ponto c é, então:
A tração pode ser decomposta em uma componente vertical e outra radial.
A componente vertical tem modulo igual ao peso, já que não há movimento nessa direção.
E a componente radial da tração faz o papel da força centrípeta.
Mas como, :
Ambos os vetores estão na mesma direção, logo esse produto vetorial vale zero.
Então nosso gabarito é a letra a! Conseguimos!
Resposta
a)