Duas partículas de mesma massa se movem sobre uma reta com velocidades constantes, de mesmo módulo e sentidos contrários. Sobre esse sistema são feitas as seguintes afirmações:

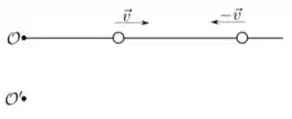
I. O momento angular de ambas as partículas com relação ao ponto é nulo

II. O momento angular de ambas as partículas com relação ao ponto é nulo

III. O momento angular total do sistema com relação aos pontos e é nulo

As afirmativas corretas são:

a) Todas as afirmativas.

b) Apenas I

c) Apenas II

d) Apenas III

e) Apenas I e II

f) Apenas I e III

g) Apenas II e III

h) Nenhuma das afirmativas.

Aqui temos velocidade, distância ao eixo e massa. As duas partículas estão distantes igualmente do novo eixo, e com velocidades contrárias, então o momento angular de cada uma vai ser diferente de zero. Essa alternativa está errada!

Vimos que, pela primeira afirmativa, o momento angular do sistema em relação ao ponto vai ser nulo, já que o momento angular de ambas as partículas em relação a esse ponto já era nulo.

Agora, em relação ao ponto , vimos pela afirmativa , que o momento angular de cada partícula em relação à era diferente de zero. Mas como ambas as partículas estão à mesma distância do novo eixo, e o módulo das velocidades é igual, temos que o módulo do momento angular delas é igual, mas como as velocidades têm sentidos opostos, os momentos angulares vão ter sinais opostos, de forma que, quando somarmos, para termos o momento angular do sistema, teremos um resultado nulo.

Então essa afirmativa está correta!