Física 1 UFRJ 3ºEE 2019.1
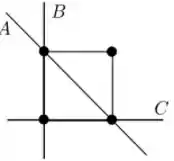
Um arame quadrado de lado , fino, rígido e de massa desprezível, tem nos seus vértices quatro massas iguais a m. Os momentos de inércia , relativos aos respectivos eixos A, B e C mostrados na figura relacionam-se como:
a)
b)
c)
d)
e)
f)
Passo 1
O momento de inércia em B e em C serão iguais, porque tem duas partículas no eixo, e as outras duas com a mesma distância (o lado do quadrado, que vale ) e com a mesma massa. Agora só falta descobrir se o momento de inércia de A é maior, menor ou igual aos outros, show? Bom, A tem duas partículas no seu eixo também, e as outras duas cada um de um lado com uma distância menor que , consequentemente é menor que a dos outros dois eixos. Conseguimos!
Resposta
a)
Exercícios de Livros Relacionados
1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu