Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética de Rotação

Ver Teoria
Exercício 341234567891011121314151617181920212223242526272829303132333536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

Física 1 UFRJ 3ºEE 2019.1

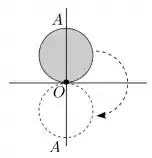
Um disco de raio R e de massa M uniformemente distribuída, possui um pequeno furo na sua periferia. Por este furo o disco é colocado no pino O, preso a uma parede vertical. No posicionamento inicial do disco o ponto A de sua periferia localizado diametralmente oposto a O está sobre o eixo vertical, acima de O; conforme mostra a figura abaixo. Como o disco está sob a condição de equilíbrio instável, ele cai girando em torno do pino O. Sabe-se que o momento de inércia I C M deste disco em torno de um eixo que passa pelo centro de massa e perpendicular e ele é igual M R 2 2 . Desprezando-se o atrito entre o pino e o disco, quando o ponto A passa pela linha vertical, abaixo de O, a velocidade angular ω do disco, é igual a:

  1. 2 2 g 3 R
  2. 2 g R
  3. g 2 R
  4. 2 g R
  5. 3 g 2 R
  6. 2 g R

Passo 1

Vamo lá! Nessa belezinha aqui podemos usar a conservação de Energia! Considerando no começo do movimento o centro de massa com altura de R em relação ao ponto O, temos:

E p = E c r o t

U = K r o t

m g h = I ω 2 2

M g 2 R = I ω 2 2

Passo 2

Como a rotação é em torno do eixo que passa pelo ponto O, precisamos saber qual é o momento de inércia em relação a esse eixo. Como fazemos isso? Pelo teorema dos eixos paralelos!

Vamos lá:

I = I C M + M d 2

Sabemos que I C M = M R 2 2 , e que a distância entre o CM e o ponto O é R. Então:

I = I C M + M d 2

I = M R 2 2   + M R 2

I = 3 M R 2 2

Agora, vamos voltar pra equação de conservação de energia.

Passo 3

M g 2 R = I ω 2 2

Substituindo o I   que achamos:

M g 2 R = 3 M R 2 ω 2 4

Isolando o ω :

ω = 8 g 3 R = 2 2 g 3 R

Prontooo! Show!

Resposta

a) 2 2 g 3 R

Exercícios de Livros Relacionados

Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que