Física 1 UFRJ 3ºEE 2019.1
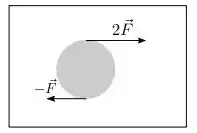
Um disco homogêneo de massa M e raio R encontra-se sobre uma mesa horizontal completamente lisa, sem estar preso a ela. Em um dado instante duas forças estão aplicadas tangencialmente na beirada do disco, uma em um ponto diametralmente oposto ao ponto de aplição da outra. Sabendo que o momento de inércia do disco relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é , e denotando por acm e α os módulos respectivos da aceleração do centro de massa do disco e da aceleração angular de rotação em torno do eixo no instante considerado, podemos dizer que:
a)
b)
c)
d)
e)
f)
Passo 1
Como sabemos, a aceleração do centro de massa depende da força que atua no corpo, como a força resultante é . Então, temos:
Pronto, já foi a primeira parte!
Passo 2
E aqui, pra calcularmos a aceleração angular, temos que:
Mas, também sabemos que o torque pode ser calculado por:
Como as duas forças atuantes no corpo estão girando o corpo para o mesmo sentido (o horário), então o torque resultante será:
Show, então substituindo lá em cima, temos que:
Como a questão nos deu o momento de inércia do corpo, temos:
Isolando a aceleração angular, que é o que queremos descobrir, ficamos com:
Conseguimosss!
Resposta
a)