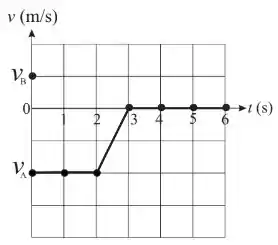
Duas partículas e , de massas e , interagem apenas entre si no intervalo . Elas deslocam-se em cima de uma mesa horizontal sem atrito ao longo do eixo . No instante , a partícula tem velocidade inicial enquanto a partícula tem velocidade inicial . Durante o intervalo de tempo observa-se, a cada segundo, a velocidade da partícula . O gráfico mostra a função obtida unindo-se por segmentos de reta os pontos experimentais representados por pequenos círculos.

Q5. Com base nos dados, determine a força média exercida pela partícula na partícula durante o tempo de colisão.

a)

b)

c)

d)

e)

Bom, o impulso de uma força é dado como:

Ou seja a multiplicação da força pelo tempo que ela atua. Quando essa força não é constante, podemos dizer que é a força média vezes o tempo que ela atua. No nosso caso, queremos:

Onde é a força média que B faz em A.

O enunciado não fala sobre quanto tempo essa colisão ocorre. Mas como podemos ver, a velocidade de B se altera entre 2 e 3 segundos, portanto, podemos considerar que essa colisão ocorreu nesse intervalo de tempo.

Voltando para o nosso teorema impulso-momento linear, teremos:

E como , ficamos com:

O momento linear da partícula é dado como:

Portanto, essa variação vai ser:

E temos que a velocidade no tempo é:

E a velocidade no tempo é:

Sendo assim, com a massa da partícula igual a , a variação do momento é:

E substituindo na expressão do teorema impulso momento, temos:

Agora para finalizar, só precisamos ficar atentos a um detalhe.A questão pediu de fato a força média que faz em . E nós encontramos a força média que faz em .

Pela terceira lei de Newton, nós podemos escrever que:

Portanto,

E assim, a resposta correta é a letra a).