Um disco homogêneo, de massa e raio , move-se no plano horizontal em rotação pura ao redor do eixo vertical fixo , que tangencia a borda do disco e é perpendicular ao plano . O vetor momento angular do disco, em relação à origem do sistema de coordenadas, é dado por , em unidades do SI. Se em , o disco está girando com velocidade angular , podemos afirmar que o seu raio , em centímetros, é:
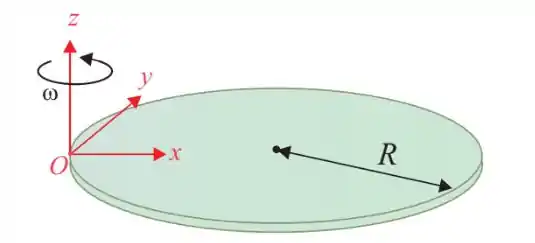
O momento de inércia de um disco de massa e raio em relação ao eixo de rotação que passa pelo seu centro de massa e é perpendicular ao plano é
a)
b)
c)
d)
e)
Passo 1
Bom galerinha.... essa é uma questão que trata do momento angular de um corpo rígido.

Bom, o cálculo do momento angular de um corpo rígido é feito como:
E podemos reparar que nessa questão, nos é informado o momento angular como uma função do tempo e nos diz que no tempo , a velocidade angular .
Só nos resta calcular o momento de inércia desse disco, e para isso precisamos tomar um cuidado adicional, pois o disco não está rotacionando ao redor do seu centro, mas sim ao redor de uma de suas extremidades.
Passo 2
Como o disco não rotacional ao redor do seu centro de massa, vamos ter que realizar o teorema dos eixos paralelos.
Ou seja, o momento de inércia em relação ao eixo é igual ao momento de inércia em relação ao centro de massa somado com a multiplicação da massa do disco pela distância ao quadrado entre o eixo de rotação e o eixo do centro de massa:
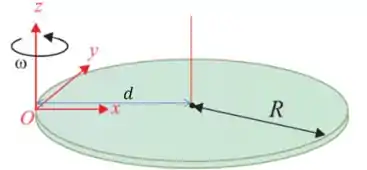
Vemos pelo desenho acima, que essa distância é igual ao raio do disco, portanto, temos:
Passo 3
Agora é só igualar esse momento de inércia com a expressão que havíamos encontrado.
E a massa do disco foi dada como .
Portanto, a resposta correta é a letra d).
Resposta
Letra d).