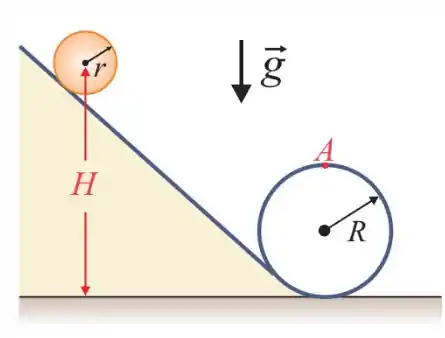
Uma bola homogênea (esfera) de raio , rola sem escorregar por um tobogã com um único de raio , como mostra a figura. A bola parte do repouso, com seu centro de massa na altura acima da base. Qual é o valor mínimo de para que a bola passe ponto no topo da volta fechada? Dê sua resposta em unidades do Sistema Internacional (SI).
O momento de inércia de uma esfera de massa e raio em relação ao eixo de rotação que passa pelo seu centro de massa e é perpendicular ao plano da página é
a)
b)
c)
d)
e)
Passo 1
Faaala galerinha... última questão da prova, pra a gente matar com chave de ouro!

Essa é uma questão de conservação de energia, com rolamento sem deslizar, com velocidade mínima para realizar um looping.
Muita coisa em uma questão só... mas vamos lá!
Em um rolamento, nós vamos ter tanto a translação quanto a rotação, por isso a energia cinética vai ser a soma das duas energias cinéticas:
E como é um rolamento sem deslizamento, podemos dizer que:
Onde é o raio da bola.
Agora, para conseguir realizar o looping, é necessário que no ponto a bola tenha uma força centrípeta mínima.
No ponto , as forças que atuam na bola são:
E ambas as forças apontam para o centro do movimento e vão ser a nossa força centrípeta:
Como queremos a velocidade mínima para realizar o looping, estamos no caso em que a normal da bola com o trilho é muito baixa, e vamos tende-la a zero.
Portanto, teremos:
Onde é o raio da trajetória circular que o centro de massa fará, portanto:
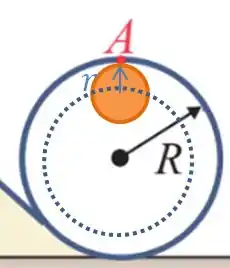
Essa é a velocidade que a bola precisa ter no ponto para conseguir realizar o looping, onde é o raio do looping. Bora lá!
Passo 2
Bom, vamos começar conservando a energia entre os pontos inicial e o ponto .
Inicialmente a bola está em repouso, então não tem energia cinética só potencial e no ponto a bola possui velocidade e está a uma certa altura do solo, portanto haverá ambas as energias.
Substituindo.
E repara que a altura é a altura do centro de massa, então teremos:
E a altura do centro de massa final, vai ser dada pelos 2 raios do looping, menos o raio da bola:
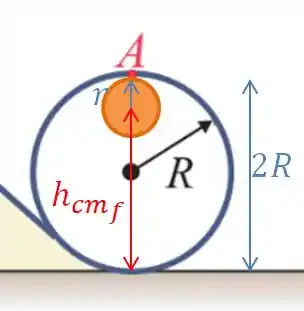
Substituindo para ficar mais simples, teremos:
Passo 3
Retornando a equação de conservação de energia:
Substituindo que , logo , temos:
E substituindo o momento de inércia da bola
Podemos cortar as massas e cortar e em uma fração.
Por fim, vamos substituir a velocidade mínima que encontramos para realizar o looping:
Podemos portanto cortar , e teremos:
Ufa, acabamos.... a resposta correta é a letra d).
Resposta
Letra d).