P-REC – Física 1 – USP – 2022 – Questão 2
Enunciado das questões Q1 e Q2
Uma partícula move-se em um plano horizontal com velocidade constante . Ao passar pelo ponto de coordenadas , no instante , ela passa a sofrer uma aceleração constante .
Q2
Qual é a distância que a partícula está em relação à origem do sistema de coordenadas, quando ? Dê sua resposta em metros.
a) 40
b) 50
c) 60
d) 70
e) 80
Passo 1
Bom galera, continuando nossa questão.
Agora queremos saber qual a distância da partícula em relação à origem quando .
Essa distância, pode ser calculada fazendo:
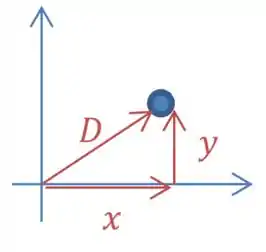
No entanto, nesse caso em específico, queremos calcular essa distância quando a coordenada vale zero, portanto:
O que faz sentido né, se a partícula não possui coordenada em , então sua distância até a origem é a própria coordenada .
Agora, qual o valor dessa coordenada ?
Bom, já encontramos na letra a) quanto tempo leva para a partícula estar na coordenada .
Agora podemos usar esse tempo para encontrar qual vai ser a coordenada da partícula nesse mesmo instante, e assim encontramos a sua distância em relação a origem.
Repara que para o eixo , nós vamos ter:
E como a aceleração é constante, teremos um MRUV no eixo . Então bora resolver esse troço...
Passo 2
Bom, sabemos que o tempo para chegar em , vale . Substituindo isso na equação da posição para o eixo teremos:
Portanto, a distância da partícula até a origem nesse instante será:
Resposta
Letra d).