P-REC – Física 1 – USP – 2022 – Questão 3
Um bloco de massa é empurrado contra uma parede por uma força que faz um ângulo com a horizontal, como mostra a figura. Se o coeficiente de atrito estático entre a superfície da parede e o bloco vale , calcule qual é o valor mínimo do módulo de que faz que o bloco permaneça estacionário. Dê sua resposta em Newtons.
Adote .
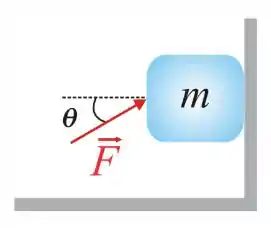
a)
b)
c)
d)
e)
Passo 1
Bom pessoal... essa questão trata do equilíbrio de forças e além disso vamos ter uma força de atrito aí...
Inicialmente, vamos fazer um diagrama de corpo livre e colocar todas as forças que atuam sobre esse bloco. Lembrando que ele tem um peso que aponta pra baixo, uma normal perpendicular a superfície e a força de atrito é contrária a iminência do movimento e paralela a superfície. Concorda comigo que essa força de atrito vai ser pra cima e vamos ter algo mais ou menos assim?
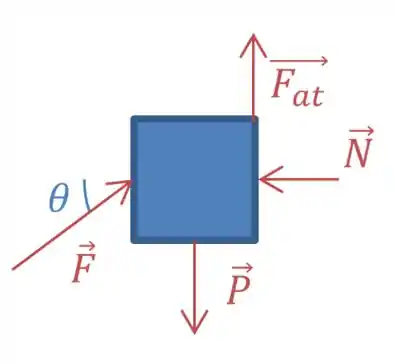
E nesse exemplo, a será a força de atrito estática máxima, pois estamos procurando pela força mínima para que o bloco não escorregue, ou seja, estamos na iminência do movimento e portanto usamos a estática máxima que é calculada fazendo normal vezes o mi estático:
Passo 2
Bom, como esse bloco está em equilíbrio, temos que as forças em são iguais a zero e as forças em também...
Considerando para a direita positivo, vamos ter:
Fazendo o equilíbrio das forças no eixo , vemos que a normal é igual a
Agora, vamos fazer o equilíbrio para o eixo .
Considerando para baixo como positivo, vamos ter:
Resolvendo para .
E substituindo os valores do enunciado, chegamos em:
Portanto, a resposta correta é a letra b).
Resposta
Letra b).