Duas partículas e , de massas e , interagem apenas entre si no intervalo . Elas deslocam-se em cima de uma mesa horizontal sem atrito ao longo do eixo . No instante , a partícula tem velocidade inicial enquanto a partícula tem velocidade inicial . Durante o intervalo de tempo observa-se, a cada segundo, a velocidade da partícula . O gráfico mostra a função obtida unindo-se por segmentos de reta os pontos experimentais representados por pequenos círculos.
Q6. Com base nos dados, determine a energia cinética do sistema formado pelas duas partículas quando e qual foi o tipo de colisão.
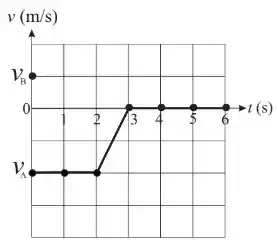
a)
b)
c)
d)
e)
Passo 1
Bom galera, continuando a nossa questão anterior, agora queremos saber qual é a energia cinética desse sistema após a colisão.
E também queremos saber se essa é uma colisão elástica ou inelástica.
Para calcular a energia cinética após a colisão, vamos realizar a conservação do momento linear, afinal para toda colisão o momento linear do sistema vai se conservar.
Realizando essa conservação, iremos encontrar a velocidade da partícula após a colisão e com isso vamos calcular a energia cinética após a colisão.
Por fim, vamos analisar se houve conservação da energia cinética ou não. Se a energia cinética após a colisão for igual a energia cinética antes, temos uma colisão elástica.
Se houve perda de energia cinética, então temos uma colisão inelástica.
Passo 2
Bom, vamos lá... conservando o momento linear nessa colisão, vamos ter:
Portanto,
Passo 3
Agora que sabemos as velocidades de e após a colisão, vamos calcular a energia cinética após a colisão.
Lembrando que , teremos:
Beleza... por fim, vamos calclar a energia cinética inicial para verificar se a colisão é elástica ou inelástica.
Opa, essa é a mesma energia que encontramos no final, portanto, houve conservação de energia e a colisão é elástica.
A resposta correta é a letra e).
Resposta
Letra e).