Um bloco de massa , que repousa sobre uma superfície horizontal lisa, é ligado a um bloco de massa por uma corda leve que passa por uma polia de massa desprezível, que pode girar sem atrito. O bloco de massa está ligado a uma mola de constante elástica que tem uma das extremidades fixa em uma parede vertical como mostra a figura. Se os blocos são liberados a partir do repouso com a mola na posição relaxada, calcule qual é a maior velocidade atingida pelos dois blocos. Dê sua resposta em metros por segundo.
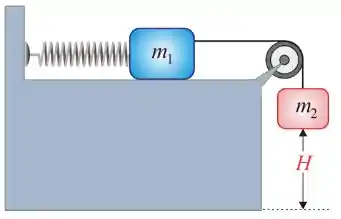
Considere os blocos como partículas.
Máximos e Mínimos de uma função são caracterizados pelo fato de que a derivada da função se anula em tais pontos.
Adote para a aceleração da gravidade
a)
b)
c)
d)
e)
Passo 1
Bom galera, essa é uma questão que tem mola, altura, velocidade dos blocos... ou seja, a cara da questão de conservação de energia né...
Só que aqui eu quero encontrar a maior velocidade que esses blocos podem alcançar...
Repara que eu só tenho o instante inicial do movimento, que é quando os blocos estão em repouso, com a mola relaxada e o bloco está a uma certa altura do solo.
Essa é a energia mecânica inicial e é essa energia que vai se conservar ao longo de todo o movimento desses blocos.
A energia mecânica para um instante qualquer do movimento desses blocos é calculada como a soma da cinética com as potenciais:
Agora, vamos considerar que esses blocos se movimentaram uma distância .
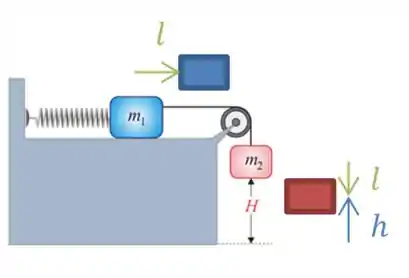
Repara que esse vai ser a própria compressão da mola, pois ela estava relaxada no início.
E que eu posso relacionar a altura final do bloco com e a altura inicial
Substituindo na expressão de energia teremos:
Passo 2
Bom, agora como a energia se conserva, vamos igualar essa expressão da energia para um momento qualquer com a energia mecânica inicial.
Resolvendo e substituindo os valores que temos, chegamos em:
Agora, eu vou escrever essa equação deixando em evidência, de forma que eu tenha em função de .
Para encontrar o , eu vou derivar essa expressão e igualar a zero. Com isso vou encontrar para o qual terei o .
Essa derivada vai ter uma regra da cadeia, por conta da raíz, então fique atento!
Substituindo na velocidade, terei:
Essa é portanto a velocidade máxima alcançada.
Resposta
Letra b).