Listas de Estudos pra Prova - Tipler Vol 1 - 6°ed de Física 1 da UTFPR - Movimento Unidimensional

(Cap 2 – Ex 10) Irmãos gêmeos idênticos estão de pé sobre uma ponte horizontal, e cada um joga uma pedra na vertical para baixo, em direção à água sob a ponte. Eles jogam as pedras exatamente ao mesmo tempo, mas uma delas atinge a água antes da outra. Como isso é possível? Explique o que eles fizeram de diferente. Ignore quaisquer efeitos da resistência do ar.

(Cap 2 – Ex 69) Uma bola é lançada verticalmente para cima do nível do chão, com uma rapidez inicial de 20 m/s. (A resistência do ar é desprezível.) (a) Quanto tempo a bola fica no ar? (b) Qual a altura máxima atingida pela bola? (c) Quantos segundos, após o lançamento, a bola estará 15 m acima do ponto de largada?

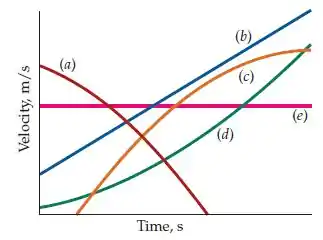
(Cap 2 – Ex 13) Qual das curvas de velocidade-versus-tempo na figura abaixo melhor descrevem o movimento de um objeto (a) com aceleração positiva constante, (b) com aceleração positiva que diminui com o tempo, (c) com aceleração positiva que aumenta com o tempo e (d) com aceleração nula. (Pode haver mais de uma resposta correta para cada item).

(Cap 2 – Ex 8) Desenhe cuidadosamente os gráficos da posição, velocidade e aceleração no mesmo intervalo de tempo para um carrinho que, sucessivamente, tem o seguinte movimento. O carrinho está se movendo à velocidade constante de na direção positiva do eixo . Ele passa pela origem em . Ele continue em diante a por , depois disso ele ganha velocidade à taxa constante de a cada segundo por . Depois de ganhar velocidade por , o carrinho perde velocidade à taxa constante de pelos próximos .

(Cap 1 – EX 57) São dados os seguintes vetores: e . (a) Encontre o vetor , em notação de vetor unitário, tal que . (b) Expresse sua resposta para a Parte (a) em termos de magnitude e ângulo com o sentido +x.

(Cap 2 – Ex 103) A velocidade de uma partícula é dada por . (a) Esboce o gráfico vs. e encontre a área sob a curva para o intervalo que vai de até . (b) Encontre a função da posição. Use-a para calcular o deslocamento durante um intervalo de até .

(Cap 2 – Ex 61) A posição de uma certa partícula depende do tempo de acordo com a equação , onde x está em metros e t está em segundos. (a) Encontre o deslocamento e a velocidade média par o intervalo . (b) Encontre a fórmula geral para o deslocamento no intervalo de tempo a . (c) Use o processo limite para obter a velocidade instantânea em qualquer tempo

(Cap 2 – Ex 75) Uma pedra é atirada verticalmente, para baixo, do topo de um pesnhasco de 200 m. Durante o último meio segundo de seu vôo, a pedra percorre uma distância de 45 m. Encontre a rapidez inicial da pedra.

(Cap 2 – Ex 60) Uma partícula se move ao longo do eixo x com a velocidade . (a) Encontre a aceleração média para dois diferentes intervalos de um segundo, um começando em e outro começando em . Esboce para o intervalo . (c) Compare as acelerações instantâneas no meio de cada um dos dois intervalos de tempo especificados na Parte (a) com as acelerações médias encontradas na Parte (a) e comente.

(Cap 2 – Ex 55) Um carro, viajando com uma rapidez constante de 20 m/s, passa por um cruzamento no tempo t=0. Um segundo carro, viajando com uma rapidez constante de 30 m/s no mesmo sentido, passa pelo mesmo cruzamento 5,0 s após. (a) Esboce as funções posição e para os dois carros para o intervalo (b) Determine quando o segundo carro ultrapassará o primeiro. (c) A que distância do cruzamento os carros estarão quando emparelharem? (d) Onde está o primeiro carro quando o segundo carro passa pelo cruzamento?

(Cap 1 – Ex 23) Nas equações a seguir, a distância está em metros, o tempo está em segundos, e a velocidade está em metros por segundo. Quais são as unidades do SI das constantes e ? (a) , (b) , (c) , (d) , (e) .