Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 2, Seção 1, Questão 13.
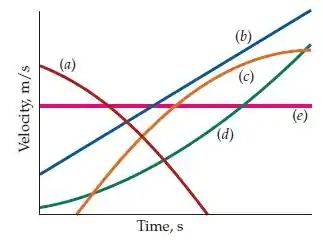
(Cap 2 – Ex 13) Qual das curvas de velocidade-versus-tempo na figura abaixo melhor descrevem o movimento de um objeto (a) com aceleração positiva constante, (b) com aceleração positiva que diminui com o tempo, (c) com aceleração positiva que aumenta com o tempo e (d) com aceleração nula. (Pode haver mais de uma resposta correta para cada item).
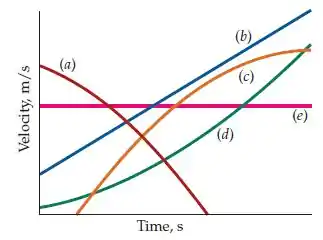
Passo 1
Falaii meus amores, show de bola?
Borá lá?
(a) Nos casos em que temos aceleração constante, a equação horária da velocidade é a seguinte:
Que é a equação de uma reta. Nos casos em que é alguma função do tempo, não temos qual saber qual será o formato do gráfico, sabemos apenas que terá algum formato diferente de uma reta.
Nesse item queremos um caso em que a aceleração é positiva e constante, ou seja, queremos uma reta de inclinação positiva, que é o caso do gráfico (b).
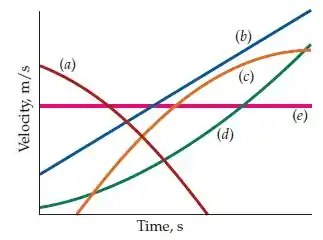
Passo 2
(b) Agora queremos um caso em que a aceleração é positiva, mas diminui com o tempo.
Se a aceleração é positiva, a velocidade tem que estar aumentando com o tempo.
Se a aceleração, além de positiva, diminui com o tempo, a inclinação do gráfico - tem que estar diminuindo.
Esse é o caso apenas do gráfico (c).
Passo 3
(c) Aqui temos um caso parecido com o do item (b), mas a inclinação tem que estar aumentando. A inclinação é sempre positiva e a aceleração variável.
Se integramos uma aceleração variável e positiva, temos
Portanto, é o caso do gráfico (d).
Passo 4
(d) No caso em que a aceleração é nula, a equação horária da velocidade fica simplesmente:
E então o gráfico é apenas uma reta horizontal. Esse é o caso do gráfico (e).
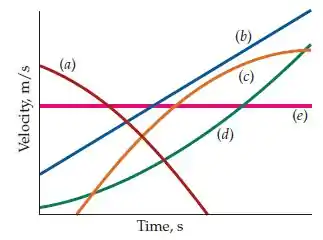
Resposta
- gráfico b; (b) gráfico c; (c) gráfico d; (d) gráfico e.
