Listas de Estudos pra Prova - Halliday Vol 1 - 8°ed de Física 1 da UTFPR - Força e Movimento

(Cap 5 – Ex 3) Apenas duas forças horizontais atuam em um corpo de que pode se mover em um piso sem atrito. Uma força é de e aponta para o leste; a outra é de e atua ao norte do oeste. Qual é o módulo da aceleração do corpo?

(Cap 5 – Ex 13) (a) Um salame de está pendurado por uma corda em uma balança de mola, que está presa ao teto por outra corda (Fig. 5 -34a). Qual é a leitura da balança, cuja escala está em unidades de peso?

(b) Na Fig. 5-34b o salame está suspenso por uma corda que passa por uma roldana e está presa a uma balança de mola. A extremidade oposta da balança está presa a uma parede por outra corda. Qual é a leitura da balança?

(c) Na Fig. 5-34c a parede foi substituída por um segundo salame de e o sistema está em repouso. Qual é a leitura da balança?

(Capítulo 5.9 – Exercício 25) Qual é o módulo da força necessária para acelerar um trenó-foguete de até em , partindo do repouso?

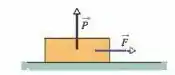
(Capítulo 5.7 – Exercício 14) Um bloco com um peso de está em repouso em uma superfície horizontal. Uma força para cima de é aplicada ao corpo através de uma mola vertical. Quais são (a) o módulo e (b) o sentido da força exercida pelo bloco sobre a superfície horizontal?

(Capítulo 5.9 – Exercício 27) Um bombeiro que pesa escorrega por um poste vertical com uma aceleração de , dirigida para baixo . Quais são (a) o módulo e (b) o sentido (para cima ou para baixo) da força vertical exercida pelo poste sobre o bombeiro e (c) o módulo e (d) o sentido da força vertical exercida pelo bombeiro sobre o poste?

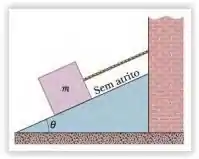
(Capítulo 5.9 – Exercício 19) Na Fig. 5-36, a massa do bloco é e o ângulo é Determine (a) a tensão na corda e (b) a força normal que age sobre o bloco. (c) Determine o módulo da aceleração do bloco se a corda for cortada.

(Cap 5 – Ex 7) Três astronautas, impulsionados por mochilas a jato, empurram e guiam um asteroide de para uma base de manutenção, exercendo as forças mostradas na Fig. 5-29, com , , , e . Determine a aceleração do asteroide

(a) em termos dos vetores unitários e como

(b) um módulo e

(c) um ângulo em relação ao semi-eixo positivo.

(Cap 5 – Ex 1) Se um corpo padrão de tem uma aceleração de a com o semi-eixo positivo, quais são

(a) a componente e

(b) a componente da força resultante a que o corpo está submetido e

(c) qual é a força resultante em termos dos vetores unitários?

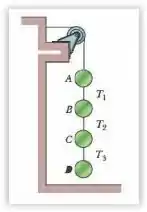
(Capítulo 5.7 – Exercício 15) A Fig. 5-33 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco , (b) do disco, (c) do disco C e (d) do disco?

(Capítulo 5.9 – Exercício 18) Tarzan, que pesa , salta de um rochedo na ponta de um cipó de que está preso ao galho de uma árvore e faz inicialmente um ângulo de com a vertical. Suponha que um eixo é traçado horizontalmente a partir da borda do rochedo e que um eixo é traçado verticalmente para cima. Imediatamente após Tarzan pular da encosta, a tensão do cipó é . Nesse instante, quais são (a) a força do cipó sobre Tarzan em termos dos vetores unitários, a força resultante sobre Tarzan (b) em termos dos vetores unitários e como (c) módulo e (d) ângulo em relação ao sentido positivo do eixo . Quais são (e) o módulo e (f) o ângulo da aceleração de Tarzan nesse instante?

(Capítulo 5.9 – Exercício 41) Um elevador que pesa move-se para cima. Qual é a tensão do cabo do elevador se a velocidade (a) está aumentando a uma taxa de e (b) está diminuindo a uma taxa de ?

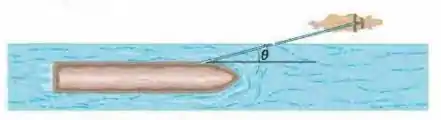
(Capítulo 5.9 – Exercício 48) No passado, cavalos eram usados para puxar barcaças em canais, como mostra a Fig. 5-42. Suponha que o cavalo puxa o cabo com uma força de módulo e ângulo em relação à direção do movimento da barcaça, que se desloca no sentido positivo de um eixo . A massa da barcaça é e o módulo da aceleração da barcaça é . Quais são (a) o módulo e (b) a orientação (em relação ao sentido positivo do eixo ) da força exercida pela água sobre a barcaça?

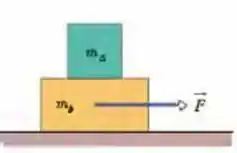
(Capítulo 5.9 – Exercício 51) Na Fig. 5-48, três blocos conectados são puxados para a direita sobre uma mesa horizontal sem atrito por uma força de módulo . Se , e , calcule (a) o módulo da aceleração do sistema, (b) a tensão e (c) a tensão

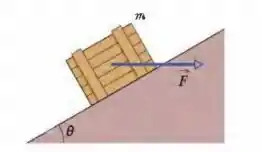
(Capítulo 5.9 – Exercício 32) Na Fig. 5-40, um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito com velocidade constante. Quais são os módulos (a) de e (b) da força que a rampa exerce sobre o caixote?

(Capítulo 5.9 – Exercício 39) Um elevador e sua carga têm uma massa total de . Determine a tensão do cabo de sustentação quando o elevador, que estava descendo a , é levado ao repouso com aceleração constante em uma distância de .

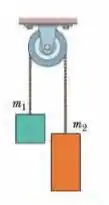
(Capítulo 5.9 – Exercício 37) Uma esfera com uma massa de está suspensa por uma corda. Uma brisa horizontal constante empurra a esfera de tal forma que a corda faz um ângulo de com a vertical. Determine (a) a força da brisa sobre a bola e (b) a tensão da corda.

(Capítulo 5.9 – Exercício 55) A Fig. 5-47 mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa ; o outro tem massa . Quais são (a) o módulo da aceleração dos blocos e (b) a tensão da corda?

(Capítulo 5.9 – Exercício 54) Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas , , . Quando o conjunto é liberado a partir do repouso, (a) qual é a tensão da corda que liga a e (b) que distância percorre nos primeiros (supondo que não atinja a polia)?

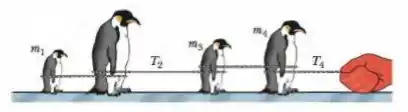
(Capítulo 5.9 - Exercício 50) A Fig. 5-49 mostra quatro pinguins que estão sendo puxados sobre gelo muito escorregadio (sem atrito) por um zelador. As massas de três pinguins e as tensões em duas das cordas são , , , e . Determine a massa do pinguim , que não é dada.

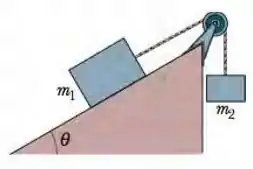
(Capítulo 5.9 – Exercício 59) Um bloco de massa sobre um plano sem atrito inclinado, de ângulo , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um outro bloco de massa (Fig. 5-52). Quais são (a) o módulo da aceleração de cada bloco, (b) o sentido da aceleração do bloco que está pendurado e (c) a tensão da corda?

(Capítulo 5.9 – Exercício 60) A fig.5-53 mostra um homem sentado em uma cadeira presa a uma corda de massa desprezível que passa por uma roldana de massa e atrito desprezível e desce de volta às mãos do homem.

A massa total do homem e da cadeira é 95,0 kg. Qual é o módulo da força com o qual o homem deve puxar a corda para que a cadeira suba

a) Com velocidade constante

b) Com uma aceleração para cima de 1,30 m/s²? (Sugestão: um diagrama do por livre pode ajudar bastante).

Se no lado direito a corda estende até o solo e é puxada por uma outra pessoa, qual é o módulo da força com a qual essa pessoa deve puxar a corda para que o homem suba.

c) Com velocidade constante

d) Com uma aceleração para cima de 1,30 m/s² ?

Qual é o módulo da força que a polia exerce sobre o teto

e) No item a

f) No item b

g) No item c

h) No item d

(Cap 6 – Ex 1) Uma cômoda com uma massa de , incluindo as gavetas e as roupas, está em repouso sobre o piso. (a) Se o coeficiente de atrito estático entre a cômoda e o piso é , qual é o módulo da menor força horizontal necessária para fazer a cômoda entrar em movimento? (b) Se as gavetas e as roupas, com uma massa total de , são removidas antes de empurrar a cômoda, qual é o novo módulo mínimo?

(Cap 5 – Ex 84) Calcule o peso de um astronauta de (a) na Terra, (b) em Marte, em que , e (c) no espaço sideral, em que. (d) Qual é a massa do astronauta em cada um desses lugares?

(Cap 5 – Ex 76) Um homem de salta para um pátio de concreto de uma janela a de altura. Ele não dobra os joelhos para amortecer o impacto e leva para parar. (a) Qual é a aceleração média desde o instante em que os pés do homem tocam o solo até o instante em que o corpo se imobiliza? (b) Qual é o módulo da força média que o pátio exerce sobre o homem?

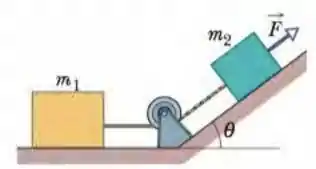
(Cap 5 – Ex 82) Na Fig. 5-64, uma força de módulo é aplicada a uma caixa de massa . A força é dirigida para cima paralelamente a um plano inclinado de ângulo . A caixa está ligada por uma corda a outra caixa de massa situada sobre o piso. O plano inclinado, o piso e a polia não tem atrito e as massas da polia e as massas da polia e da corda são desprezíveis. Qual é a tensão da corda?

(Cap 5 – Ex 86) Uma pessoa de salta de paraquedas e experimenta uma aceleração para baixo de . A massa do paraquedas é . (a) Qual é a força para cima que o ar exerce sobre o paraquedas? (b) Qual é a força que a pessoa exerce sobre o paraquedas?

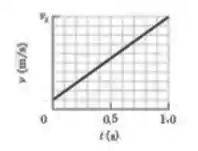
(Cap 6 – Ex 18) Um bloco de é empurrado sobre um piso por uma força horizontal constante de módulo . A Fig. 6-30 mostra a velocidade do bloco em função do tempo quando o bloco se desloca sobre o piso ao longo de um eixo . A escala vertical do gráfico é definida por . Qual é o coeficiente de atrito cinético entre o bloco e o piso?

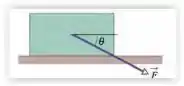
(Cap 6 – Ex 7) Um bloco de é empurrado ao longo de um piso horizontal por uma força de módulo que faz um ângulo com a horizontal (Figura 6-19). O coeficiente de atrito cinético entre o bloco e o piso é . Calcule (a) o módulo da força de atrito que o piso exerce sobre o bloco e (b) o módulo da aceleração do bloco.

(Cap 6 – Ex 5) O piso de um vagão de trem está carregado de caixas soltas cujo coeficiente de atrito estático com o piso é . Se o trem está se movendo inicialmente com uma velocidade de , qual é a menor distância na qual o trem pode ser parado com aceleração

constante sem que as caixas deslizem no piso?

(Capítulo 5 – Problemas Adicionais – Exercício 73) Um operário arrasta um caixote no piso de uma fábrica puxando-o por uma corda. O operário exerce uma força de módulo sobre a corda, que está inclinada de um ângulo em relação à horizontal, e o chão exerce uma força horizontal de módulo que se opõe ao movimento. Calcule o módulo da aceleração do caixote (a) se a massa do caixote é e (b) se o peso do caixote é .

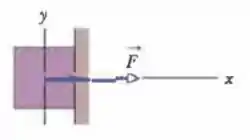
(Cap 6 – Ex 17) Uma força horizontal de empurra um bloco de de peso contra uma parede vertical (Fig. 6-26). O coeficiente de atrito estático entre a parede e o bloco é e o coeficiente de atrito cinético é . Suponha que o bloco não esteja se movendo inicialmente. (a) O bloco vai se mover? (b) Qual é a força que a parede exerce sobre o bloco em termos dos vetores unitários?

(Cap 6 – Ex 15) O coeficiente de atrito estático entre o Teflon e ovos mexidos é cerca de . Qual é o menor ângulo com a horizontal que faz com que os ovos deslizem no fundo de uma frigideira revestida com Teflon?

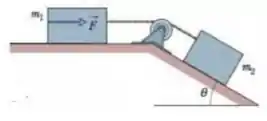
(Capítulo 5.9 – Exercício 66) A Fig. 5-56 mostra uma caixa de massa sobre um plano inclinado sem atrito de ângulo . Ela está ligada por uma corda de massa desprezível a uma caixa de massa sobre uma superfície horizontal sem atrito. A polia não tem atrito e sua massa é desprezível. (a) Se o módulo da força horizontal é , qual é a tensão da corda? (b) Qual é o maior valor que o módulo de pode ter sem que a corda fique frouxa?

(Cap 6 – Ex 16) Você depõe como perito em um caso envolvendo um acidente no qual o carro bateu na traseira de um carro que estava parado em um sinal vermelho no meio de uma ladeira (Fig. 6-25). Você descobre que a inclinação da ladeira é , que os carros estavam separados por uma distância quando o motorista do carro freou bruscamente, bloqueando as rodas (o carro não dispunha de freios ABS), e que a velocidade do carro no momento em que o motorista pisou no freio era . Com que velocidade o carro bateu no carro se o coeficiente de atrito cinético era (a) 0,60 (estrada seca) e (b) (estrada coberta de folhas molhadas)

(Cap 6 – Ex 6) Um porco brincalhão escorrega em uma rampa com uma inclinação de e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?

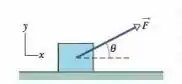
(Cap 6 – Ex 14) A Fig. 6-20 mostra um bloco inicialmente estacionário de massa sobre um piso. Uma força de módulo é aplicada com um ângulo para cima. Qual é o módulo da aceleração do bloco se (a) e e (b) e ?

(Cap 6 – Ex 9 ) Um bloco de está inicialmente em repouso em uma superfície horizontal. Uma força horizontal de módulo e uma força verticalsão aplicadas ao bloco Os coeficientes de atrito entre o bloco e a superfície são e. Determine o módulo da força de atrito que age sobre o bloco se o módulo de é (a) (b) e (c)

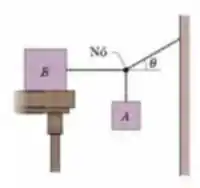
(Cap 6 – Ex 23) O bloco da Fig. 6-31 pesa . O coeficiente de atrito estático entre o bloco e a mesa é ; o ângulo é ; suponha que trecho da corda entre o bloco e o nó é horizontal. Determine o peso máximo do bloco para o qual o sistema permanece em repouso.

(Cap 6 – Ex 44) Suponha que o coeficiente de atrito estático entre a estrada e os pneus de um carro é e não há sustentação negativa. Que velocidade deixa o carro na iminência de derrapar quando faz uma curva não compensada com de raio?

(Cap 6 – Ex 43) Um gato está cochilando em um carrossel parado, a uma distância de do centro. O brinquedo é ligado e logo atinge a velocidade normal de funcionamento, na qual completa uma volta a cada . Qual deve ser, no mínimo, o coeficiente de atrito estático entre o gato e o carrossel para que o gato permaneça no mesmo lugar, sem escorregar?

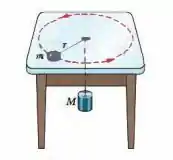
(Cap 6 – Ex 55) Um disco de metal de massa descreve uma circunferência de raio sobre uma mesa sem atrito enquanto permanece ligado a um cilindro de massa pendurado por um fio que passa por um furo no centro da mesa (Fig. 6-43). Que velocidade do disco mantém o cilindro em repouso?

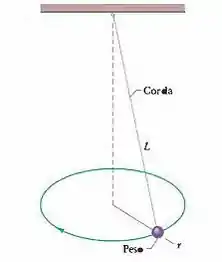
(Cap 6 – Ex 60) A Fig. 6-53 mostra um pêndulo cônico, no qual um peso (pequeno objeto na extremidade inferior da corda) se move em uma circunferência horizontal com velocidade constante. (A corda descreve um cone quando o peso gira.) O peso tem uma massa de , a corda tem um comprimento e a massa desprezível e o peso descreve uma circunferência de . Determine (a) a tensão da corda e (b) o período do movimento.

(Cap 6 – Ex 49) Um estudante que pesa está sentado, com as costas eretas, em uma roda-gigante em movimento. No ponto mais alto, o módulo da força normal exercida pelo assento sobre o estudante é . (a) O estudante se sente mais leve ou mais pesado neste ponto? (b) Qual é o módulo de no ponto mais baixo? Se a velocidade da roda-gigante é duplicada, qual é o módulo da força normal (c) no ponto mais alto e (d) no ponto mais baixo?

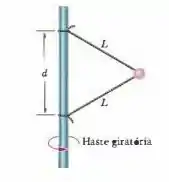
(Cap 6 – Ex 59) Na Fig. 6-45, uma bola de é ligada por meio de dois fios de massa desprezível, cada um com comprimento , a uma haste vertical giratória. Os fios estão amarrados à haste a uma distância um do outro e estão esticados. A tensão do fio de cima é . Determine (a) a tensão do fio de baixo; (b) o módulo da força resultante a que está sujeita a bola; (c) a velocidade escalar da bola; (d) a direção de

(Cap 6 – Ex 51) Um bonde antigo dobra urna esquina fazendo uma curva plana com de raio a . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?

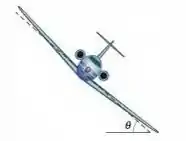
(Cap 6 – Ex 53) Um avião está voando em uma circunferência horizontal com uma velocidade de (Fig. 6-41). Se as asas estão inclinadas de um ângulo com a horizontal, qual é o raio da circunferência? Suponha que a força necessária para manter o avião nessa trajetória resulte inteiramente de uma "sustentação aerodinâmica" perpendicular à superfície das asas.

(Cap 6 – Ex 29) O bloco da Fig. 6-33 pesa e o bloco pesa . Os coeficientes de atrito entre e a rampa são e . O ângulo é igual a . Suponha que o eixo é paralelo à rampa, com o sentido positivo para cima. Em termos dos vetores unitários, qual é a aceleração de se está inicialmente (a) em repouso, (b) subindo a rampa e (c) descendo a rampa?

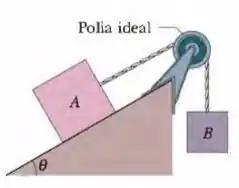
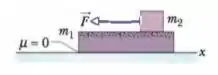
(Cap 6 – Ex 27) Dois blocos, com e de peso, estão ligados por uma corda sem massa e deslizam para baixo em um plano inclinado de . O coeficiente de atrito cinético entre o bloco mais leve e o plano é e o coeficiente de atrito cinético entre o bloco mais pesado e o plano é . Supondo que o bloco mais leve desce na frente, determine (a) o módulo da aceleração dos blocos e (b) a tensão da corda.

(Cap 6 – Ex 34) Na Fig. 6-37, uma prancha de massa repousa em um piso sem atrito e um bloco de massa repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é e o coeficiente de atrito cinético é . O bloco é puxado por uma força horizontal de módulo . Em termos dos vetores unitários, qual é a aceleração (a) do bloco e (b) da prancha?

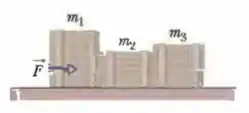
(Cap 6 – Ex 28) A Fig. 6-32 mostra três caixotes sendo empurrados sobre um piso de concreto por uma força horizontal de módulo . As massas dos caixotes são , e . O coeficiente de atrito cinético entre o piso e cada um dos caixotes é de . (a) Qual é o módulo da força exercida sobre o bloco pelo bloco ? (b) Se os caixotes deslizassem sobre um piso polido, com um coeficiente de atrito cinético menor que , o módulo seria maior, menor ou igual ao valor quando o coeficiente de atrito era ?

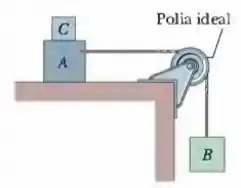
(Cap 6 – Ex 31 ) Na Fig. 6-34, os blocos e pesam e , respectivamente. (a) Determine o menor peso do bloco que evita que o bloco deslize, se entre e a mesa é . (b) O bloco é removido bruscamente de cima do bloco . Qual é a aceleração do bloco se entre e a mesa é ?

(Cap 6 – Ex 64) Na Fig. 6-50, o bloco 1, de massa , e o bloco 2, de massa , estão ligados por um fio de massa desprezível e são inicialmente mantidos em repouso. O bloco 2 está sobre uma superfície sem atrito com uma inclinação . O coeficiente de atrito cinético entre o bloco 1 e a superfície horizontal é . A polia tem massa e atrito desprezíveis. Ao serem liberados, os blocos entram em movimento. Qual é a tensão do fio?

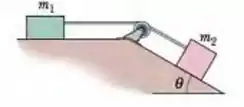
(Cap 6 – Ex 63) Na Fig. 6-54, o coeficiente de atrito cinético entre o bloco e o plano inclinado é e o ângulo . Quais são (a) o módulo e (b) o sentido (para cima ou para baixo ao longo do plano) da aceleração do bloco se ele está escorregando para baixo? Quais são (c) o módulo e (d) o sentido da aceleração se o bloco está escorregando para cima?

(Cap 6 – Ex 76) Calcule o módulo da força de arrasto a que está sujeito um míssil de de diâmetro voando a em baixa altitude. Suponha que a massa específica do ar é e o coeficiente de arrasto é .

(Cap 6 – Ex 101) Quando uma pequena moeda de é colocada a uma distância de do centro de um prato giratório horizontal que executa três rotações completas em , a moeda não escorrega. Determine (a) a velocidade escalar da moeda, (b) o módulo e (c) o sentido (radialmente para dentro ou para fora) da aceleração da moeda e (d) o módulo e (e) o sentido (para dentro ou para fora) da força de atrito sobre a moeda. A moeda fica na iminência de escorregar quando é colocada a uma distância de do centro. (f) Qual é o coeficiente de atrito estático entre a moeda e o prato giratório?

(Cap 6 – Ex 65) Um bloco de massa é colocado em cima de um outro bloco de massa . Para fazer o bloco de cima deslizar sobre o bloco de baixo enquanto o segundo é mantido fixo, é preciso aplicar ao bloco de cima uma força horizontal de no mínimo . O conjunto de blocos é colocado sobre uma mesa horizontal sem atrito (Fig. 6-47). Determine o módulo (a) da maior força horizontal que pode ser aplicada ao bloco de baixo sem que os blocos deixem de se mover juntos e (b) a aceleração resultante dos blocos.