Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 2, Seção 1, Questão 103.
(Cap 2 – Ex 103) A velocidade de uma partícula é dada por . (a) Esboce o gráfico vs. e encontre a área sob a curva para o intervalo que vai de até . (b) Encontre a função da posição. Use-a para calcular o deslocamento durante um intervalo de até .
Passo 1
Falaii galerinha do Responde ai, belezinha?
Bora analisar mais uma?
A velocidade de uma partícula pode ser calculada substituindo os valores do tempo na função de velocidade dada. Agora a área sob a curva pode ser calculada usando o gráfico. O deslocamento da partícula pode ser calculado integrando a função de velocidade dada dentro dos intervalores de tempos dados.
(a) Queremos fazer o gráfico da seguinte função:
Essa é uma função de primeiro grau, então o nosso gráfico será uma reta com inclinação e que cruza o eixo vertical no ponto .
Para desenhar isso no papel você pode fazer o seguinte, desenho o plano - e marque dois pontos quaisquer da função, por exemplo:
Portanto, o gráfico entra a velocidade e o tempo da partícula é mostrado na figura a seguir:
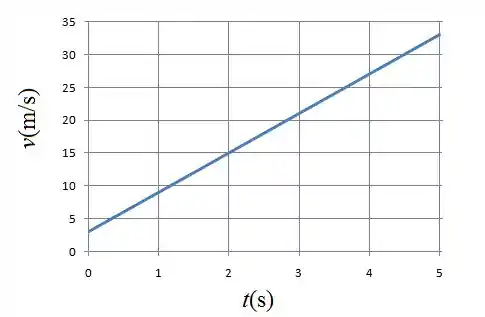
Passo 2
E o enunciado pediu para calcularmos a área sob esse gráfico no intervalo que vai de até .
Nesse caso, a área sob o gráfico tem o formato de um trapézio, e temos que usar a seguinte fórmula para calcular a área:
E nesse caso:
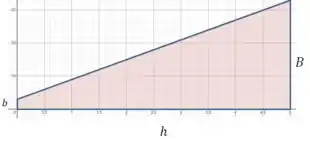
E olhando mais perto no gráfico vemos que e , então:
Passo 3
(b) Vamos lembrar da relação entre a velocidade e a posição:
Ou, tomando o caminho contrário:
Então vamos integrar a função dada pelo enunciado para encontrar a função da posição:
Passo 4
E agora vamos usar essa função para calcular o deslocamento no intervalo até :
E então o deslocamento total é:
Resposta
(a) A área sob o gráfico resulta em .
(b) .