P1 de Física 2 da UFRJ - 2012.2

Um objeto de densidade está boiando num fluido de densidade quando este se encontra à temperatura . O fluido é então resfriado para a temperatura , causando em aumento em sua densidade, que agora vale . A densidade do objeto não se altera com o resfriamento. Sabendo-se que a fração do volume do objeto fora do fluido à temperatura é , qual a nova fração , agora à temperatura ?

Considere um tubo em formato de “U”, cujos “braços” são dois cilindros verticais de seções transversais circulares de áreas e . Ambas extremidades são mantidas abertas. No interior deste tubo coloca-se uma quantidade de líquido cuja massa total e densidade são e , respectivamente. Este líquido é inicialmente deslocado para fora do equilíbrio , gerando-se um desnível na altura do líquido nos dois braços do “U” mas de forma tal que as superfícies livres sejam mantidas horizontais. A partir de então, o líquido inicia oscilações livres, sob ação da gravidade . Suponha que a amplitude de oscilação seja pequena comparada com o comprimento do tubo e que as superfícies livres do líquido se movem sempre nas seções puramente verticais do tubo.

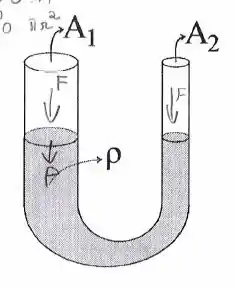
1. Desprezando os efeitos da viscosidade, calcule o período de oscilações do líquido para o caso particular em que .
2. Ainda desprezando os efeitos da viscosidade, generalize o resultado do item anterior para o caso genérico .
3. Discuta de maneira qualitativa e em palavras, pelo menos 2 alterações diferentes que devem ocorrer neste movimento oscilatório ao incluirmos os efeitos da viscosidade. Seja conciso em sua resposta.

Um recipiente parcialmente cheio de um líquido de densidade é equilibrado em um prato de uma balança de dois pratos. Um cubo de lado é pendurado em um fio e mergulhado inteiramente neste líquido, sem tocar o fundo do recipiente e sem provocar transbordamento. Qual massa deve ser acrescentar (ou retirada) do outro lado da balança para reestabelecer o equilíbrio?

1. Deve ser retirada uma massa
2. Não há necessidade de alterar a massa, pois o sistema permanece em equilíbrio
3. Deve ser acrescentada uma massa de
4. Deve ser acrescentada uma massa tal que a total seja
5. Depende da força no fio que sustenta o cubo

A densidade de um corpo é ligeiramente menor do que a da água. No entanto, ele é muito mais compressível. O que acontecerá se ele for colocado próximo à superfície e se for colocado a uma grande profundidade, respectivamente?

1. Ele afundará no primeiro e no segundo
2. Ele boiará na superfície no primeiro caso e no segundo
3. Ele boiará na superfície no primeiro caso e afundará no segundo
4. Ele afundará no primeiro caso e boiará no segundo
5. Ele boiará na superfície no primeiro caso e no segundo, mas com uma fração maior fora d’água no segundo caso

Três carros trafegam sobre uma mesma reta e com velocidades de mesma magnitude em relação ao solo. Os carros 1 e 3 trafegam contra o vento. O carro 2 trafega a favor do vento, que tem velocidade de módulo em relação ao solo. Ao avistar o carro 2, o motorista do carro 1 pressiona a buzina de seus carro, emitindo uma onda sonora de frequência em seu referencial. Sendo e as frequências do som da buzina do carro 1 percebidas pelos motoristas dos carros 2 e 3, respectivamente, podemos afirmar:

Uma corda homogênea e inextensível de comprimento e densidade linear de massa é tensionada por um bloco de massa , como mostrado na figura. A extremidade esquerda da corda está ligada a um anel de massa desprezível, o qual pode deslizar sem atrito em uma haste vertical. Considere o eixo apontado para direita com origem na posição do anel e suponha que ondas transversais sejam produzidas na corda usando-se uma fonte externa de frequência variável (não indicada na figura). Suponha conhecida a velocidade da onda nesta corda sob estas condições e que a corda não descole da roldana em nenhum momento.

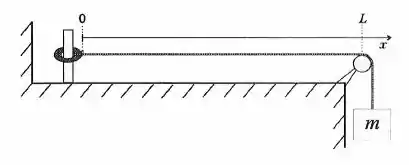
1. Mostre que , onde , e são constantes, é solução da equação de ondas unidimensional (não é necessário deduzi-la) e determine a relação entre , e .
2. Utilizando as condições de contorno e determine o comprimento de onda do n-ésimo modo normal de vibração.
3. Esboce os três modos normais de vibração de menor frequência observados na corda.
4. Calcule a frequência e o comprimento de onda do modo normal de vibração de menor frequência observado na corda se o anel é mantido fixo à haste.

Um bebê alegra-se gritando de felicidade e saltando para cima e para baixo em seu berço. Sua massa é de e o colchão do berço pode ser modelado como uma mola leve com constante de força de . Para que o movimento do bebê possua máxima amplitude, qual deve ser a frequência aplicada por ele ao colchão? (adote )

Um fluido incompressível de densidade escoa com velocidade por uma tubulação horizontal cilíndrica de raio inicial . A tubulação tem um estrangulamento, passando a ter raio , sendo . A tubulação é estreita o suficiente para que possamos desprezar diferenças de altura entre as linhas de corrente. Se a diferença de pressão entre os trechos 1 e 2 é ,qual o valor de ?

Uma onda plana harmônica de comprimento , amplitude e freqüência propaga-se numa superfície líquida. No instante observa-se uma partícula, que bóia nesta superfície, na coordenada vertical . Qual será sua coordenada em ?

Consideramos uma mola com 2 constantes elásticas: , quando é esticada e , quando comprimida:

Suponha que esta mola seja presa a um bloco de massa que pode oscilar sobre uma superfície horizontal sem atrito. O período de oscilação do sistema é:

Suponha que um vento com velocidade sopre sobre o telhado de uma casa, de seção reta com área . Qual o peso mínimo do telhado para evitar que este se solte? Suponha conhecida a densidade do ar.

Uma forma de medir a massa de um objeto em uma estação espacial é o seguinte: primeiro, o astronauta mede a frequência de oscilação de um sistema elástico de massa conhecida. Depois, a massa desconhecida é adicionada a esse sistema e uma nova medida de frequência de oscilação é tomada. Qual o valor de ?