Equação de Bernoulli
Suponha que um vento com velocidade sopre sobre o telhado de uma casa, de seção reta com área . Qual o peso mínimo do telhado para evitar que este se solte? Suponha conhecida a densidade do ar.
Passo 1
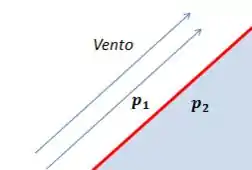
Vamos considerar a parte azul do desenho abaixo o interior da casa, que tem uma pressão , e a parte que não tem cor como o exterior, onde passa o vento, e que tem pressão
A parte vermelha representa o telhado:
Passo 2
O deslocamento do vento do lado de fora causa uma diferença de pressão. A partir dessa diferença de pressão que vamos calcular o peso mínimo que o telhado tem que ter.
Vamos usar Bernoulli entre o lado de fora e o de dentro, considerando que eles tem a mesma altura e que no lado de dentro o ar está parado:
Show? Achamos uma diferença de pressão.
Passo 3
Essa diferença de pressão que vai gerar uma força no telhado que fará ele levantar, caso ele não seja pesado o suficiente. Como o telhado tem área
O peso tem que ser igual a essa força:
b)
Resposta
b)