Empuxo-Princípio de Arquimedes
Um recipiente parcialmente cheio de um líquido de densidade é equilibrado em um prato de uma balança de dois pratos. Um cubo de lado é pendurado em um fio e mergulhado inteiramente neste líquido, sem tocar o fundo do recipiente e sem provocar transbordamento. Qual massa deve ser acrescentar (ou retirada) do outro lado da balança para reestabelecer o equilíbrio?
- Deve ser retirada uma massa
- Não há necessidade de alterar a massa, pois o sistema permanece em equilíbrio
- Deve ser acrescentada uma massa de
- Deve ser acrescentada uma massa tal que a total seja
- Depende da força no fio que sustenta o cubo
Passo 1
Bom galera, o que acontece aqui é o seguinte:
A balança estava equilibrada, mas alguém inseriu um novo corpo dentro do fluido.
Então, surge uma nova força atuando em um dos lados da balança. Qual é essa força?
Passo 2
Quando o bloco é inserido no liquido, surge uma força de empuxo que o empurra pra cima, aplicada pelo fluido. Pela lei da ação e reação, o próprio corpo aplica uma força de mesmo modulo e direção, mas de sentido contrário no fluido.
Mais ou menos isso aqui: Na esquerda é o fluido agindo no corpo e na direita o corpo no fluido:
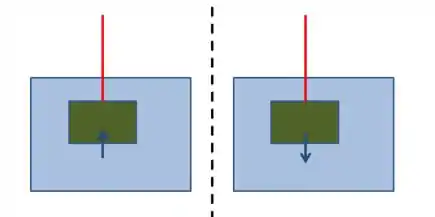
Passo 3
Então é esse força extra sentida pelo fluido que a balança vai sentir. E o valor da massa que vamos ter que colocar do outro lado, e não retirar, dependerá disso:
Calculando o empuxo sofrido pelo corpo:
Show? Então quanto vale a massa? Encarando a força acima como um peso, fica fácil descobrir:
c)
Resposta
c)