Considere um tubo em formato de “U”, cujos “braços” são dois cilindros verticais de seções transversais circulares de áreas e . Ambas extremidades são mantidas abertas. No interior deste tubo coloca-se uma quantidade de líquido cuja massa total e densidade são e , respectivamente. Este líquido é inicialmente deslocado para fora do equilíbrio , gerando-se um desnível na altura do líquido nos dois braços do “U” mas de forma tal que as superfícies livres sejam mantidas horizontais. A partir de então, o líquido inicia oscilações livres, sob ação da gravidade . Suponha que a amplitude de oscilação seja pequena comparada com o comprimento do tubo e que as superfícies livres do líquido se movem sempre nas seções puramente verticais do tubo.
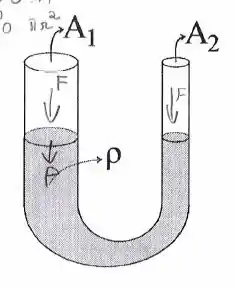
- Desprezando os efeitos da viscosidade, calcule o período de oscilações do líquido para o caso particular em que .
- Ainda desprezando os efeitos da viscosidade, generalize o resultado do item anterior para o caso genérico .
- Discuta de maneira qualitativa e em palavras, pelo menos 2 alterações diferentes que devem ocorrer neste movimento oscilatório ao incluirmos os efeitos da viscosidade. Seja conciso em sua resposta.
Passo 1
a):
O pequeno desnível de altura vai gerar um efeito assim:

Como nesse primeiro caso a as áreas são iguais, o desnível de altura da esquerda vai ser igual ao da direita, só que em um o líquido sobe e no outro o líquido desce.
Então, será gerada um desnível total de , de um lado pro outro.
Passo 2
Qual a pressão causada por isso? Vai ser:
E qual a força que vem dessa pressão? Em uma área, será:
Mas como temos duas áreas, teremos:
Legal! O que você precisa entender aqui é isso: Essa força vai ser a força restauradora do MHS que vai surgir nesse fluido. Como todo o fluido vai oscilar, essa vai ser a força que seria como a força elástica num movimento com uma mola.
Por isso, como fazemos com molas, vamos por um menos na frente da força. Além disso, vamos chamar . Assim, a força vai estar no modelo de uma força elástica.
Então:
Legal, chegamos numa EDO de um MHS. Agora, é só você lembrar que o termo que acompanha o é a frequência angular ao quadrado:
E como:
Passo 3
b):
Agora, como as áreas são diferentes, as alturas dos desníveis também serão diferentes:
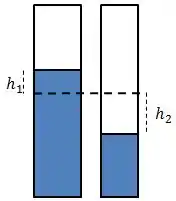
Assim, a pressão total, pelo teorema de Stevin, será:
Mas, tem como eu escrever em função de ? Tem, como o fluido é incompressível, o volume deslocado tem que ser o mesmo. Então a gente pode usar isso:
Assim:
Passo 4
Legal, temos a pressão total. E as forças? Vamos calcular em cada área e somar:
Show! Agora é só a gente tratar essa força como uma força elástica, reescrevendo ela assim:
Passo 5
Agora só seguir aquele caminho:
Então:
Passo 6
c):
O primeiro efeito é que a viscosidade vai gerar um atrito. Então, o movimento oscilatório deixa de ser um MHS e passa a ser um MHA.
O outro efeito é que a viscosidade pode causar um escoamento não laminar das partículas do fluido. O escoamento passa a ser turbulento, ou seja, não vai se enquadrar naquele capitulo de linhas de fluido da gente.
Resposta
a):
b):
c):
O primeiro efeito é que a viscosidade vai gerar um atrito. Então, o movimento oscilatório deixa de ser um MHS e passa a ser um MHA.
O outro efeito é que a viscosidade pode causar um escoamento não laminar das partículas do fluido. O escoamento passa a ser turbulento, ou seja, não vai se enquadrar naquele capitulo de linhas de fluido da gente.