USP – Física 2 – 2019 – P1 – Exercício 3
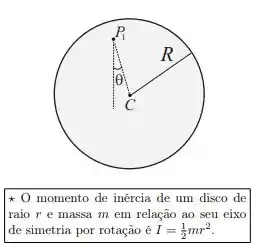
Um pêndulo, constituído por um disco fino de massa e raio , e centro de massa em C, é pendurado por um ponto a uma eixo fixo, conforme mostra a figura. O disco pode balançar livremente, de um lado para outro, quando é deslocado, de um ângulo , a partir de sua posição de equilíbrio. Se o movimento do pêndulo é restringido a ângulos pequenos, e a distância entre o ponto de suspensão e o centro de massa é , o período das oscilações quando ele oscila em torno do ponto é:
a)
b)
c)
d)
e)
Passo 1
Pronto para uma questão de prova sobre MHS? Essa é muito boa para você revisar algumas coisas de física 1!
Queremos achar o período do pêndulo constituído por um disco fino que oscila preso no ponto . Vamos ter que calcular o torque exercido pelo peso do disco sobre o ponto e lembrar de física 1 que
Para calcular o torque, considere a figura:
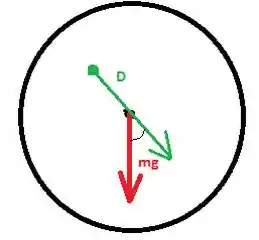
O vetor torque é dado por
Nesse caso, como só queremos o módulo:
O sinal de vemo do fato de ser torque restaurador! Assim,
Passo 2
Para ângulos pequenos, temos que . Assim, obtemos uma equação de MHS:
A frequência angular é dada por
Lembre-se que pelos dados do problema e . Vamos focar agora no momento de inércia!
O enunciado disse que o momento de inércia do disco com relação ao seu centor de massa C é
Para achar o momento de inércia com relação ao ponto , usamos o teorema dos eixos paralelos:
Assim,
Passo 3
Para achar o período:
Assim,
Colocando o para dentro da raiz:
A resposta é alternativa B!
Resposta
Alternativa B.