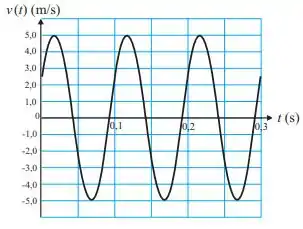
O gráfico mostra a velocidade em função do tempo de uma partícula de massa , ligada a uma mola, que move-se em movimento retilíneo sobre uma mesa horizontal sem atrito, realizando um MHS. A velocidade inicial da partícula é . A expressão do deslocamento da partícula em função do tempo é:

a)

b)

c)

d)

e)

Note que é a amplitude da velocidade, que também é a velocidade máxima do movimento:

Do gráfico tiramos que

Com isso,

Já temos que

Falta descobrir a fase .

Sabemos que . Assim,

Nossas opções são

Essas são os ângulos nos terceiro e quarto quadrantes, respectivamente. Como saber qual deles é o correto? Vamos olhar para a posição:

Se , então ; caso , temos .

Note que em a velocidade é positiva e está aumentando até que atinge seu máximo em e daí passa a diminuir, seguindo positiva mas diminuindo até se anular próximo de (esse é um ponto de retorno). Como a velocidade era positiva nesse trecho, o corpo se movia no sentido positivo da trajetória. Antes de , a partícula estava em e a partir daí (após atingir o máximo de ) passa a se mover com até atingir o ponto de retorno onde a velocidade muda de sinal. Com isso, para , a posição é negativa. Logo, , de modo que .

Portanto, a função horária da posição é

Alternativa C 😊