USP – Física 2 – 2019 – P1 – Exercício 1
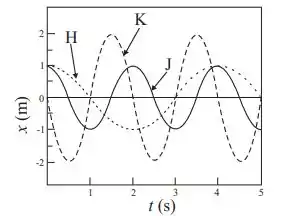
Os três gráficos da figura ao lado representam a posição em função do tempo, , de partículas realizando diferentes movimentos harmônicos simples, identificados pelas letras H, K e J. Se as velocidades máximas das partículas são dadas por , e para os movimentos H, K e J, respectivamente, e , e são as respectivas frequências angulares dos movimentos, podemos afirmar que:
a) e .
b) e .
c) e .
d) e .
e) e .
Passo 1
Fala galera, vamos resolver essa questão sobre MHS da POLI!
O problema forneceu o gráfico da posição de três partículas executando um MHS. O primeiro passo é identificar a amplitude e o período de cada movimento.
Para achar a amplitude, você procurar o máximo no gráfico da posição: a amplitude será o valor máximo da posição (ou o mínimo em módulo, da no mesmo). Para achar o período, procure uma oscilação completa na figura e veja qual o comprimento dessa oscilação no eixo horizontal!
Para o movimento H:
Para K:
E para J:
Passo 2
Sabemos que a frequência angular é dada por
onde é a frequência, que é dada pelo inverso do período:
Assim,
Desta forma, para H:
Como :
Portanto,
Com isso já conseguimos eliminar três alternativas: as únicas que restam são A e D!
Passo 3
Agora vamos olhar para a velocidade de cada um. Sabemos que a posição é dada por
onde é a amplitude, é a frequência angular e é uma fase que não vai fazer diferença aqui. Portanto, a velocidade é
A velocidade é máxima quando for . Assim,
Para H:
Para K:
Para J:
Portanto,
Com isso, a única alternativa que nos resta é D 😊
Resposta
Alternativa D.