USP – Física 2 – 2019 – P1 – Exercício 4
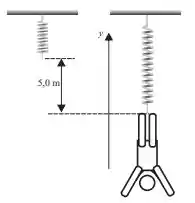
Um malabarista de está pendurado por uma corda com constante elástica de , que pode ser modelada como uma mola. Ele é puxado para baixo, até um ponto em que a corda está mais comprida do que seu comprimento não esticado, e depois é liberado a partir desta posição. Adotando o eixo mostrado na figura e considerando que as oscilações verticais do malabarista constituem um MHS unidimensional, a posição do malabarista como função do tempo, medida a partir da posição de equilíbrio do malabarista, é:
a)
b)
c)
d)
e)
Passo 1
Eai pessoal, vamos resolver mais uma questão sobre MHS! Nessa aqui, um malabarista está executando um MHS e temos que descrever o movimento em torno da posição de equilíbrio. Com isso, o primeiro passo é determinar onde é a posição de equilíbrio em que a força da mola cancela o peso do malabarista:
Assim,
Usando que estava no formulário da prova:
Com isso, a posição de equilíbrio está abaixo da mola relaxada:
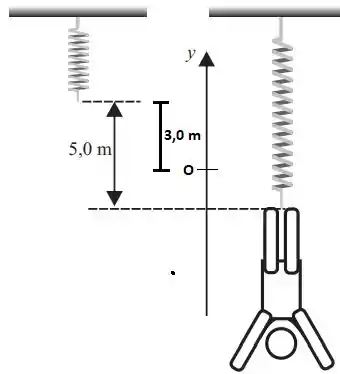
Passo 2
Em , o malabarista está na posição e com . A posição é essa pois a deformação é , a mais a que deformação de equilíbrio, que é nossa referência! Além disso, o malabarista está abaixo da origem e o eixo aponta para cima, por isso a coordenada é negativa!
A equação horária da posição é
A velocidade é obtida pela derivada da posição:
Para , temos :
Para , temos :
Como , temos que
Com isso, . Por simplicidade, vamos escolher de modo que . Com isso,
Portanto, a equação horária da posição é
Passo 3
Para achar :
Como e :
Portanto,
Com isso, a resposta está na alternativa B!
Resposta
Alternativa B.