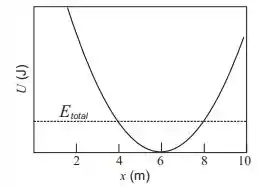
A figura ao lado é o diagrama de energia potencial para uma trajetória de massa , que está sujeita à força conservativa , onde . A partícula é liberada do repouso na posição , com energia mecânica total , represnetada na figura por uma linha horizontal tracejada. Com base nestas informações podemos afirmar que a equação horária que descreve a velocidade da partícula em , é:
a)
b)
c)
d)
e)
Passo 1
Fala galera, prontos para mais um problema de MHS da POLI?
A questão forneceu um diagrama de energia para o movimento. Note que o mínimo do potencial ocorre em , e olhando para onde a energia mecânica total corta o gráfico, vemos que o corpo oscila entre e . Já conseguimos tirar daí que a amplitude é .
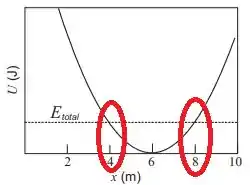
A equação horária da posição é do tipo
O representa a posição de equilíbrio e a amplitude. Quando , a posição é ; e quando , a posição é .
Derivando nós achamos a velocidade:
Passo 2
Para uma partícula de massa executando um MHS presa a uma mola de constante elástica , sabemos que
Como e :
Muito cuidado para não deixar a massa em gramas!!!
Já temos que
Passo 3
Para achar , usamos a informação que em a partícula está em repouso na posição . Assim,
Desta forma,
Portanto,
A resposta está na alternativa B 😊
Passo 4
O problema podia perguntar também qual é a energia mecânica total do sistema, então só pra treinar, vamos calculá-la! A energia mecânica é a soma da energia cinética com a potencial:
Você pode colocar as expressões para e na equação acima que você vai chegar na resposta, mas existe um jeito muito mais legal!
A energia mecânica do sistema se conserva, então podemos escolher um instante de tempo particular para usar a fórmula. Vamos escolher um instante que a deformação da mola é máxima, de modo que e . Assim,
Substituindo os valores:
Note que poderíamos escolher também o instante em que (deformação da mola é nula) e a velocidade é máxima: . Assim,
Note que essa é uma forma de relacionar a amplitude da velocidade com a amplitude do movimento:
Tudo que eu discuti nesse passo é desnecessário para esse problema, mas é sempre bom saber desses truques 😉
Resposta
Alternativa B.