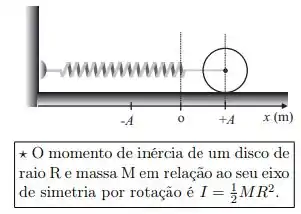
Uma mola de constante elástica tem uma extremidade fixada numa parede e a outra, no centro de um disco de massa M, que pode movimentar-se numa superfície horizontal. No instante inicial, o disco está em repouso na posição de equilíbrio. A partir da posição de equilíbrio, o disco é puxado para a direita até que a elongação da mola seja . Depois de solto a partir da posição , o disco rola sem deslizar, realizando um movimento harmônico simples. A frequência angular do movimento é:
a)
b)
c)
d)
e)
Passo 1
Esse é meu exercício favorito de toda a P1 de 2019 e eu vou te explicar por que!
Ele fala que o cilindro rola sem deslizar e executa um MHS preso à mola. Queremos saber qual a frequência do MHS. Para isso poderíamos considerar as forças agindo no disco e usar a segunda lei de Newton, caindo numa equação diferencial que daria . Mas nesse caso isso ia ser bem complicado, então vamos fazer de um jeito diferente que eu particularmente amo muito 😊
A sacada aqui é escrever uma expressão para a energia mecânica, que terá três termos: a energia cinética de translação, a energia cinética de rotação e a energia potencial elástica da mola.
A energia cinética de translação do disco é dada por
Já a energia cinética de rotação é
onde é a velocidade angular de rotação do disco. Não confundir (frequência angular do MHS) com (velocidade angular de rotação do disco)! A energia potencial elástica armazenada na mola é
Somando as três parcelas obtemos a energia mecânica:
Passo 2
Para que haja rolamento sem deslizamento, existe uma relação entre e :
Para entender melhor isso, veja a figura:
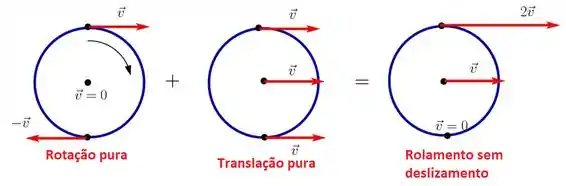
Para uma rotação pura, todos os pontos da extremidade do disco terão uma velocidade de rotação dada por
Essa velocidade é sempre tangente ao disco!
Já na translação pura, todos os pontos de movem para a direita com velocidade . O movimento de rolamento é a soma dos dois movimentos. No ponto de contato com o solo, a velocidade é
Para que haja deslizamento sem rolamento, a velocidade desse ponto de contato deve ser nula:
Além disso, o enunciado deu
Desta forma,
Portanto,
Essa é a expressão para a energia do sistema em função de e . Mas como
podemos escrever
Passo 3
Até aqui foi só física 1, agora que vem a brincadeira legal! Vamos derivar essa equação com relação ao tempo! Não se esqueça de usar a regra da cadeia! Derivando o primeiro termo:
Para o segundo termo:
Juntando tudo:
Colocando em evidência:
Como o rolamento é sem deslizamento, podemos garantir que a energia mecânica é conservada. Assim,
já que ela não varia com o tempo. Assim,
Portanto,
Para transformação essa equação na EDO do MHS, multiplicamos toda equação por :
Essa é exatamente uma equação de MHS do tipo
Portanto,
A resposta está na alternativa A!
Olha que bonitinho que foi: usamos apenas a conservação da energia para obter a equação diferencial do MHS. Podemos fazer isso em muitos problemas, então nunca esquece esse método: sempre que for complicado demais usar as leis de Newton para achar a equação, esse método pode ser muito útil!
Resposta
Alternativa A.