P3 de Física 2 da USP - 2019

Na primeira fileira de um show de rock você escutaria a música ser tocada com . O máximo nível de intensidade que um celular emite é . Quantos celulares (no volume máximo) você iria precisar para escutar música no mesmo volume que seria o show de rock?

a) .

b) .

c) .

d) .

e) .

f) .

g) nenhuma das respostas indicadas.

Marcos está tentando afinar o seu violão. Depois de ajustar a corda (primeira corda) para , ele começa a trabalhar na segunda corda (). Ao bater nas duas cordas simultaneamente ele nota um batimento ocorrendo a uma taxa de batidas a cada segundos. Quando tocada separadamente, a corda produz um som mais agudo. Podemos afirmar que a corda está afinada com a frequência de:

a) .

b) .

c) .

d) .

e) .

f) .

g) nenhuma das respostas indicadas.

Duas cordas de diferentes densidades lineares de massa estão bem esticadas e unidas no ponto . Ao fazer na corda uma onda harmônica (onda incidente), cria-se uma onda na corda (onda refratada), e uma onda no sentido oposto na própria corda (onda refletida). Se e são as velocidades das ondas nas cordas e , respectivamente, e a razão entre as amplitudes das ondas refletida e incidente é , a razão entre as intensidades das ondas refratada e incidente é:

a)

b)

c)

d)

e)

f)

g) nenhuma das respostas indicadas.

Uma onda que se propaga ao longo de uma corda ideal apresenta a velocidade de fase ( ) igual à velocidade de grupo (). Porém, quando se considera uma corda real, a dependência da frequência angular com o número de onda pode ser descrita pela relação de dispersão:

onde é uma constante positiva que depende das propriedades mecânicas da corda e é a tensão aplicada na corda de densidade linear de massa . Se a razão entre a velocidade de fase e a velocidade de grupo é para uma onda com número de onda , para uma corda de densidade sujeita a uma tensão , o valor da constante , no sistema SI, é:

a) .

b) .

c) .

d).

e) .

f) .

g) nenhuma das respostas indicadas.

No arranjo mostrado na figura, uma massa está pendurada em uma das extremidades de uma corda, de densidade linear de massa igual a , e que passa sobre uma polia leve. Na outra extremidade da corda, um oscilador senoidal coloca a corda em movimento com uma frequência constante de . Observa-se que os elementos da corda situados nos pontos e estão aproximadamente em repouso, com deslocamento quase nulo durante o movimento de vibração da corda, de modo que eles podem ser considerados como nós.

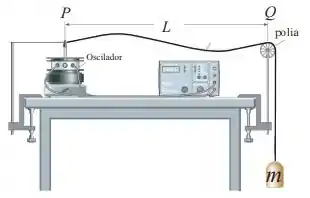
Podemos afirmar que o -ésimo modo normal que se estabelece na corda quando a distância entre os pontos e é é: (Use )

a) .

b) .

c) .

d)

e) .

f) .

g) nenhuma das respostas indicadas.

Quando uma raquete de tênis acerta uma bola, ela começa a vibrar. As vibrações têm frequências bem definidas, que dependem do tamanho da raquete e do padrão de vibração. Considere uma raquete, representada na figura ao lado, vibrando no padrão com uma frequência de .

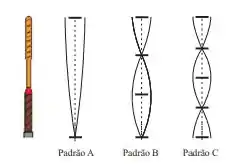
Podemos afirmar que nos padrões e ela vibrará com as seguintes frequências, respectivamente:

a) e .

b) e .

c) e .

d) e .

e) e .

f) e .

g) nenhuma das respostas indicadas.

Uma onda estacionária transversal produzida numa corda de comprimento infinito tem as seguintes características: o deslocamento de um ponto da corda em em função do tempo está descrito na figura ao lado e, além disso, o ponto é um ventre e o primeiro nó da onda se localiza em .

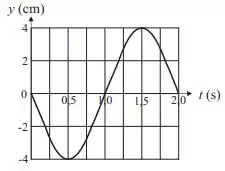
Determine a função que descreve o deslocamento da corda em função do tempo, com todos os valores numéricos pertinentes.

Duas ondas se propagam em uma mesma corda horizontal muito comprida. Uma das ondas, que se propaga para a esquerda no sentido , é dada por

e a outra onda, que se propaga para a direita no sentido , é dada por

onde e estão dados em metros e em segundos. A superposição das ondas cria uma onda estacionária. Seja a posição do primeiro ventre da corda tal que . A posição no instante é:

a) .

b) .

c) .

d) .

e) .

f) .

g) nenhuma das respostas indicadas.