No arranjo mostrado na figura, uma massa está pendurada em uma das extremidades de uma corda, de densidade linear de massa igual a , e que passa sobre uma polia leve. Na outra extremidade da corda, um oscilador senoidal coloca a corda em movimento com uma frequência constante de . Observa-se que os elementos da corda situados nos pontos e estão aproximadamente em repouso, com deslocamento quase nulo durante o movimento de vibração da corda, de modo que eles podem ser considerados como nós.
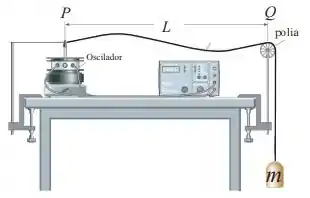
Podemos afirmar que o -ésimo modo normal que se estabelece na corda quando a distância entre os pontos e é é: (Use )
a) .
b) .
c) .
d)
e) .
f) .
g) nenhuma das respostas indicadas.
Passo 1
Fala galerinha, prontos para uma questão super clássica sobre ondas em cordas? Partiu!!!
O primeiro passo em problemas assim é achar a velocidade de propagação da onda na corda. Para isso, lembre-se que
onde é a tensão no fio e é a densidade linear de massa da corda. Para achar a tensão você deve olhar para a massa presa a corda. Pelo equilíbrio de forças agindo sobre a massa, a tensão da corda deve igualar o peso:
Assim,
Usei que foi dado na questão! Assim,
Portanto,
Ou ainda,
Passo 2
Agora vamos olhar para a corda vibrando de forma estacionária com os pontos e em repouso. Para isso, considere a figura:
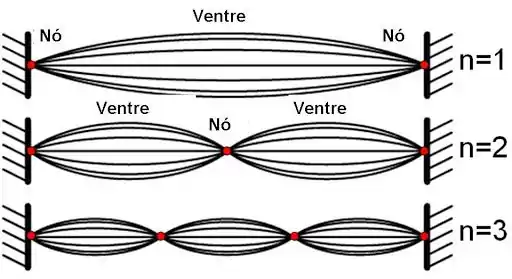
Note que representa o número de fusos (ou “quibes”) da onda estacionária. Cada fuso tem um comprimento
Assim, o tamanhos total da corda é o número de fusos vezes o tamanho de um fuso:
Portanto,
Como
Temos que
Passo 3
Substituindo os valores:
Ou ainda,
Note que esse número nem é inteiro. Dessa forma, essa corda não consegue vibrar de forma estacionária com essa frequência. Só nos resta assinalar a alternativa G 😊
Resposta
Alternativa G.