Duas cordas de diferentes densidades lineares de massa estão bem esticadas e unidas no ponto . Ao fazer na corda uma onda harmônica (onda incidente), cria-se uma onda na corda (onda refratada), e uma onda no sentido oposto na própria corda (onda refletida). Se e são as velocidades das ondas nas cordas e , respectivamente, e a razão entre as amplitudes das ondas refletida e incidente é , a razão entre as intensidades das ondas refratada e incidente é:
a)
b)
c)
d)
e)
f)
g) nenhuma das respostas indicadas.
Passo 1
Fala pessoal? Prontos para mais uma questão sobre ondas em corda? Nesse problema vamos discutir um pouco os conceitos de reflexão, refração e intensidade!
A primeira coisa que você deve saber é que a intensidade de uma onda é proporcional ao quadrado da amplitude:
Assim, se as duas ondas estiverem se propagando na mesma corda (com mesma densidade e mesma velocidade), a razão das intensidades será igual ao quadrado da razão das amplitudes:
Vamos precisar disso mais para frentes!
Passo 2
Considere o esquema a seguir: um pulso incidente caminha em direção ao ponto de encotro das cordas. Quando ele chega lá, dois pulsos se forma: um pulso refletido que caminha na mesma corda e um pulso refratada que caminha na outra corda!
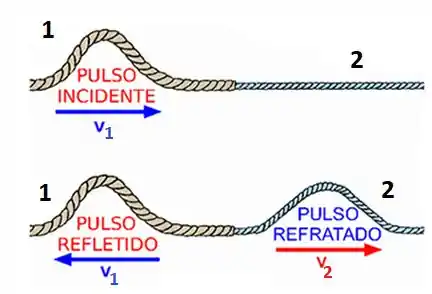
Como o pulso incidente e o pulso refletido estão na mesma corda, temos que
Mas o enunciado disse que
Portanto,
Passo 3
Além disso, você deve lembrar que a intensidade de uma onda está diretamente relacionada com sua potência. Assim, por conservação de energia, a intensidade da onda incidente deve ser igual a soma das intensidades das ondas refletidas e refratadas:
Dividindo tudo por :
Portanto,
A razão do lado esquerdo representa a porcentagem da energia no pulso refratado e a razão do lado direito representa a porcentagem da energia no pulso refletido. A soma das duas razões é ().
Como sabemos que
Temos que
Assim,
Mas
Portanto,
Essa expressão está na alternativa A 😊
Resposta
Alternativa A.