Uma onda estacionária transversal produzida numa corda de comprimento infinito tem as seguintes características: o deslocamento de um ponto da corda em em função do tempo está descrito na figura ao lado e, além disso, o ponto é um ventre e o primeiro nó da onda se localiza em .
Determine a função que descreve o deslocamento da corda em função do tempo, com todos os valores numéricos pertinentes.
Passo 1
Prontos para mais uma questão sobre ondas estacionárias? Vamos lá!
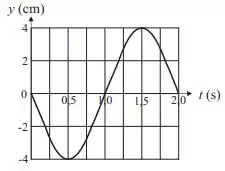
Temos uma onda estacionária e o enunciado deu o gráfico de como função do tempo na posição . Assim, o gráfico fornecido é da função com :
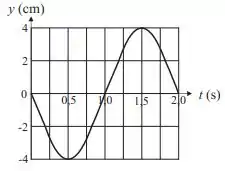
Desse gráfico, conseguimos tirar o período (tempo para que ocorre uma oscilação completa):
Assim, como
temos que
Passo 2
A expressão geral de uma onda estacionária é do tipo
As constantes e são, respectivamente, o número de onda e a frequência angular. e são outras constante que devemos determinar!
Fazendo , obtemos a expressão do gráfico fornecido pela questão:
Para achar , basta ver que o máximo do gráfico ocorre em . Assim,
Além disso, para , temos que :
Assim, ou . Como escolher entre eles?
Passo 3
Para saber se ou , vamos olhar para a velocidade:
No ponto :
Fazendo :
Agora olhe para o gráfico. No ponto , para imediantamente após , o deslocamento é negativo logo depois de ser nulo. Isso siginifica que a velocidade (taxa de variação da velocidade) é negativa nesse instante:
Portanto,
Com isso, obtemos pois e . Já temos, portanto,
Passo 4
Só nos resta achar ! O enunciado disse que o primeiro nó (ponto com para qualquer ) está em . Assim,
Portanto,
Logo,
Assim, a função fica
Se você quiser, pode lembrar que
Assim,
Essa é a resposta da questão!