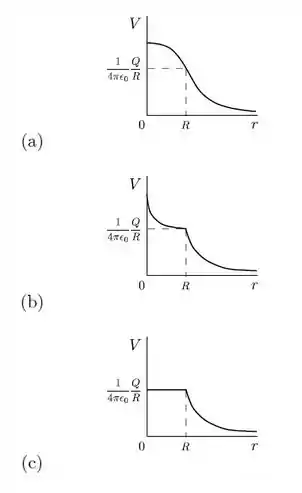
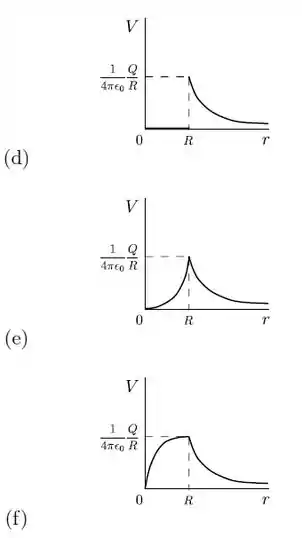
Qual dos gráficos abaixo melhor representa o potencial eletrostático de uma esfera de raio e carga uniformemente distribuída em todo o seu interior, supondo o potencial zero no infinito?
Passo 1
Como os gráficos são diferentes somente na parte interior à esfera vamos estudar essa parte somente. A fórmula que precisamos para calcular o potencial eletrostático é a seguinte:
Ok, para poder utilizar ela, precisamos da fórmula do campo elétrico dentro da esfera, coisa que nós não temos. Vamos descobrir pela Lei de Gauss. Como não é discursiva não precisamos justificar nada, portanto:
Onde é a área da Gaussiana e é a carga interna à ela.
Passo 2
Portanto, vamos calcular essa carga interna pela integral, como sempre fazemos:
A integral do volume vai ser o volume de uma esfera de raio
Substituindo a densidade de carga, que é constante:
Passo 3
Substituindo tudo:
Agora podemos integrar essa beleza aí, partindo da superfície da esfera e indo para um ponto dentro dela .
Passo 4
Para não confundir, vamos chamar essa bagunça constante toda de , então segue que:
OK, chegamos à seguinte coisa:
A única coisa que precisamos fazer agora é identificar qual tipo de curva essa é. Ora bolas, é uma parábola, do tipo:
Ou seja, com a concavidade voltada para baixo.
Temos duas opções assim: a e f! Pra tirar essa dúvida vamos ver o potencial na origem
Ou seja, é maior que . Agora matamos! A única opção que obedece isso é a letra a!
Resposta
Letra a