Uma esfera, de raio e carga total , possui uma densidade volumar (resultante) de carga estacionária, mas não uniforme, dada por:
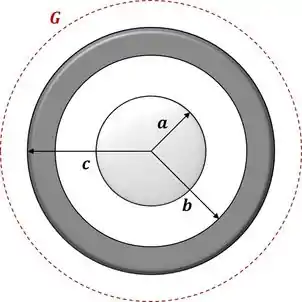
Onde é uma constante e é a distância até o seu centro. Essa esfera está envolta por uma casca esférica condutora, concêntrica, de raio interno e raio externo , com carga total , em equilíbrio eletrostático.
- Expresse a constante como função de e de .
- Quais são as densidades superficiais de carga na casca esférica condutora?
- Determine o campo elétrico nas quatro regiões:
- Determine o potencial eletrostático nas quatro regiões supracitadas, tomando-o como zero no infinito.
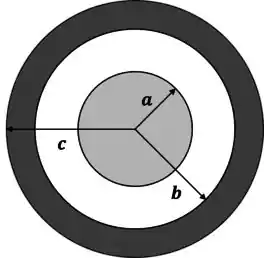
Passo 1
Essa primeira se trata de uma questão de calcular a carga total. Como temos uma densidade volumar, temos:
Integrando em toda a esfera:
Passo 2
Sabemos também que:
Substituindo:
Portanto:
Como se queria o em função das outras constantes, isolamos:
Passo 3
Agora resolvemos a clássica questão das densidades superficiais. Temos que o condutor tem carga total , portanto, por conservação de cargas:
: Carga na superfície externa
: Carga na superfície interna
Na parte maciça do condutor não pode haver campo além de que a carga interna à Gaussiana é proveniente da esfera maciça e da carga da superfície interna , portanto, pela Lei de Gauss:
Passo 4
Aplicando na equação de conservação de cargas:
Agora basta dividir pelas áreas para obter as densidades:
Analogamente:
Passo 5
Dando prosseguimento, agora partimos para calcular o campo em todas as regiões. Na primeira região, vemos um corte da Gaussiana, que é uma esfera:
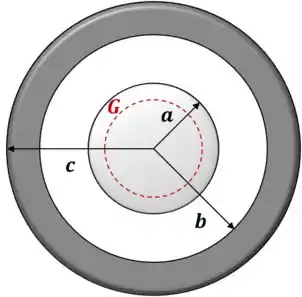
Enunciamos a Lei de Gauss:
Onde, por conta da configuração do campo, que é radial e possui simetria esférica, a nossa é escolhida como uma esfera de raio arbitrário .
Em função disto, em toda ela o vetor é paralelo ao vetor , portanto:
Além disso, ainda em função da configuração do campo, o módulo deste é constante em toda :
Logo podemos tirar o campo da integral:
Segue que:
Nos resta calcular a carga interna à Gaussiana.
Passo 6
Integrando a densidade vezes o diferencial de volume em toda a Gaussiana, obtemos a quantidade de carga interna à ela:
Ao passo que sabemos o valor da constante :
Substituindo na expressão do campo e multiplicando pelo vetor diretor :
Passo 7
Já na segunda região:
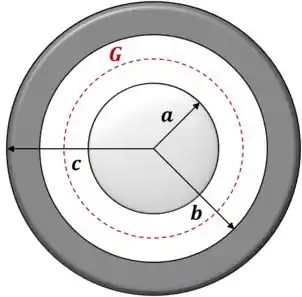
Analogamente ao passo 3, nós escolhemos uma Gaussiana esférica de raio arbitrário , logo:
Ao passo que a carga interna é a carga total da esfera de raio :
Substituindo e multiplicando pelo vetor diretor:
Passo 8
Agora estamos na terceira região:
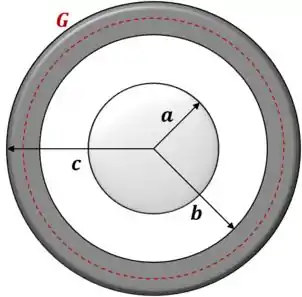
De acordo com o enunciado estamos dentro de um condutor em equilíbrio eletrostático, portanto o campo é necessariamente nulo:
Passo 9
Finalmente, fazemos a quarta e última região:
Analogamente ao passo 3, pela Lei de Gauss, escolhemos uma Gaussiana esférica de raio arbitrário , portanto:
A carga interna é a soma de todas as cargas, portanto:
Logo:
Passo 10
Aplicando a equação da diferença de potencial eletrostático:
Escolhendo um caminho radial partindo do infinito e chegando à um ponto na região , temos que o paralelismo entre e some com aquele produto escalar:
Integra:
E obtemos o nosso potencial para :
Passo 11
Agora passamos para a região . Como temos que partir de um ponto de potencial conhecido, vamos partir de :
Onde o é obtido pela expressão anterior:
E o campo nós obtivemos do Passo 9:
Obtemos então nossa expressão do potencial nessa região:
Passo 12
Mesmo esquema. Vamos para a região . Partindo de até um ponto arbitrário, o campo nós obtivemos do Passo 8:
O potencial nós tiramos na expressão anterior:
Substituindo , dá no mesmo porque não depende de :
Arrumando, obtemos o nosso potencial para a região :
Passo 13
Partindo agora para a última região . Saímos do ponto onde conhecemos o potencial, e o campo nós tiramos do Passo 7:
O potencial vem do passo anterior:
Quando for ficando feio assim acho que não tem problema substituir :
Se quiser arrumar, à vontade:
Ufa, enfim!
Resposta
- e