P1 de Física 3 da UFRJ - 2015.1

Uma superfície imaginária esférica fechada envolve completamente um dipolo elétrico e nenhuma outra partícula carregada. Podemos afirmar que:

o campo elétrico é zero em todos os pontos da superfície.

o campo elétrico possui módulo constante em todos os pontos da superfície.

o campo elétrico é normal à superfície em todos os seus pontos.

o fluxo do campo elétrico através de uma parte da superfície pode não ser igual a zero.

o fluxo do campo elétrico através da superfície não pode ser igual a zero, pois há cargas envolvidas pela mesma.

Considere um cubo uniformemente carregado com densidade volumar . Um aluno deseja calcular o campo elétrico em um ponto fora do cubo e para isso resolve usar a lei de Gauss traçando uma superfície gaussiana cúbica que passa pelo ponto . Ele faz as seguintes afirmações sobre o problema:

A lei de Gauss vale nessa situação;

Para usar a lei de Gauss, basta escolher uma superfície gaussiana que tenha a mesma simetria do objeto em questão;

Tendo o objeto e a superfície gaussiana simetria cúbica, é possível afirmar que o campo é constante sobre a superfície gaussiana.

Qual(is) delas é(são) verdadeira(s)?

Nenhuma.

Somente a .

Somente a .

Somente a .

Somente a e a .

Somente a e a .

Somente a e a .

Todas.

O potencial elétrico em uma região do espaço é dado por , onde é uma constante não nula.

Deduza uma expressão para o campo elétrico na região.

Deduza o trabalho realizado pela força elétrica sobre uma partícula de carga , quando esta é deslocada do ponto até o ponto .

Seja agora uma região esférica, centrada na origem, de raio . Qual a carga no interior dessa superfície?

Obs.: você pode achar útil escrever o campo em coordenadas esféricas.

Considere as seguintes afirmativas:

Partículas carregadas, no exterior de uma superfície fechada , não contribuem nem para o fluxo do campo elétrico através de , nem para o campo elétrico resultante em pontos de ;

Se o fluxo do campo elétrico através de uma superfície fechada for zero, não há partículas carregadas no interior de tal superfície;

A lei de Gauss só vale para distribuições de carga simétricas.

Qual(is) delas é(são) verdadeira(s)?

Nenhuma.

Somente a .

Somente a .

Somente a .

Somente a e a .

Somente a e a .

Somente a e a .

Todas.

Duas partículas de cargas e , separadas pela distância , produzem um potencial no ponto .

Traz-se então uma terceira partícula do infinito até o ponto . Sabendo-se que o potencial gerado pelas 3 partículas é nulo no infinito, pode-se concluir que:

O campo elétrico gerado apenas por e deve ser zero em .

O trabalho total para aproximar as partículas de carga e do infinito até a distância é zero.

O trabalho realizado pela força elétrica ao trazer-se a terceira carga do infinito para o ponto é zero.

A força elétrica exercida por e sobre é zero.

A energia potencial desse sistema de 3 cargas é zero.

Dois bastões idênticos, finos, de mesmo comprimento , estão dispostos nos semi-eixos positivos e conforme mostra a figura. Neles, há uma distribuição de carga estacionária, não necessariamente uniforme, com a mesma densidade linear, onde é a distância de um ponto genérico sobre um dos bastões até a origem.

Considere dois elementos infinitesimais, nos pontos e , dos bastões em e , com comprimentos e , respectivamente.

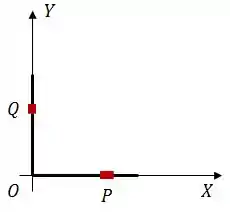
Qual é a força elétrica que o elemento em exerce sobre o elemento em ?

Considere um semi-anel circular, fino, de raio , situado no plano , conforme mostra a figura. Suponha que a densidade linear de carga de tal semi-anel seja dada por

onde é o tradicional ângulo polar, medido no sentido anti-horário, a partir do eixo .

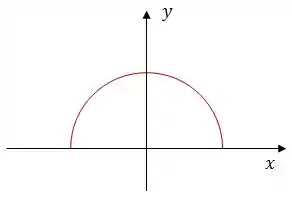
Qual é a carga elétrica total, , do semi-anel?

Calcule o campo elétrico na origem.

Calcule o potencial eletrostático em um ponto qualquer do eixo , com cota (Sabendo-se que o potencial no infinito é nulo).

Que componente(s) do campo elétrico, no mesmo ponto mencionado no item , pode(m) ser deduzida(s) a partir do resultado obtido no item anterior? Justifique e deduza-a(s).

Três partículas pontuais de cargas , e estão localizadas respectivamente nos pontos de coordenadas , e num sistema de eixos cartesianos . Sabendo que , são os vetores unitários nas respectivas direções e , podemos dizer que a forca resultante na partícula de carga devida às outras duas partículas têm a direção e sentido do vetor.

Considere um capacitor de duas placas paralelas (com vácuo entre elas), inicialmente separadas por uma distância e submetidas a uma voltagem . Alguém então dobra a voltagem entre as placas, mantendo a distância de separação.

Conclui-se então que:

A capacitância na nova configuração é o dobro da configuração inicial.

A capacitância na nova configuração é a metade da configuração inicial.

A capacitância na nova configuração é o quádruplo da configuração inicial.

A capacitância não se altera, pois ela é independente da voltagem aplicada.

Nenhuma das afirmativas anteriores está correta.

Desejamos colocar três partículas pontuais, cujas cargas são dadas por e , nos vértices de um triângulo equilátero. Considere que inicialmente as partículas estavam no infinito e infinitamente distantes entre si.

O que podemos dizer sobre o trabalho necessário para montar essa configuração?

Ele depende da ordem com que trazemos as partículas.

Ele independe da ordem, mas depende das trajetórias pelas quais trazemos as partículas.

Ele independe da ordem e das trajetórias, mas depende do valor de .

Ele independe de qualquer coisa, pois, pela simetria da disposição das cargas, o trabalho é nulo.

Nenhuma das afirmativas anteriores está correta.