Energia Potencial e Densidade de Energia
Desejamos colocar três partículas pontuais, cujas cargas são dadas por e , nos vértices de um triângulo equilátero. Considere que inicialmente as partículas estavam no infinito e infinitamente distantes entre si.
O que podemos dizer sobre o trabalho necessário para montar essa configuração?
Ele depende da ordem com que trazemos as partículas.
Ele independe da ordem, mas depende das trajetórias pelas quais trazemos as partículas.
Ele independe da ordem e das trajetórias, mas depende do valor de .
Ele independe de qualquer coisa, pois, pela simetria da disposição das cargas, o trabalho é nulo.
Nenhuma das afirmativas anteriores está correta.
Passo 1
A configuração é, basicamente essa:
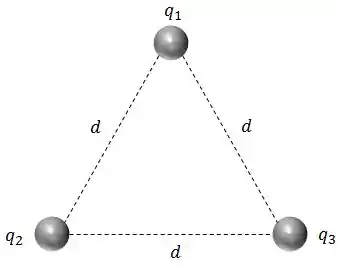
O trabalho necessário para montar essa configuração será:
Onde e .
Ok, agora vamos analisar cada alternativa separadamente.
Passo 2
Ele depende da ordem com que trazemos as partículas.
Quando calculamos o trabalho realizado, fizemos:
Logo, o trabalho independe da ordem que as partículas são trazidas.
A afirmativa é falsa.
Passo 3
Ele independe da ordem, mas depende das trajetórias pelas quais trazemos as partículas.
No cálculo do trabalho, nos preocupamos apenas com o ponto inicial e com o ponto final, nunca demos a mínima para a trajetória.
A afirmativa é falsa.
Passo 4
Ele independe da ordem e das trajetórias, mas depende do valor de .
A expressão final do trabalho que encontramos foi:
Logo, o trabalho depende do valor de .
A afirmativa é verdadeira.
Passo 5
Ele independe de qualquer coisa, pois, pela simetria da disposição das cargas, o trabalho é nulo.
Bom, já calculamos o trabalho e vimos que ele não é nulo, logo, a afirmativa é falsa.
Passo 6
Nenhuma das afirmativas anteriores está correta.
Já matamos que a alternativa certa é a letra , então nem vamos ligar pra essa opção.
Resposta
Ele independe da ordem e das trajetórias, mas depende do valor de .