Forças Elétricas, Densidade de Carga
Dois bastões idênticos, finos, de mesmo comprimento , estão dispostos nos semi-eixos positivos e conforme mostra a figura. Neles, há uma distribuição de carga estacionária, não necessariamente uniforme, com a mesma densidade linear, onde é a distância de um ponto genérico sobre um dos bastões até a origem.
Considere dois elementos infinitesimais, nos pontos e , dos bastões em e , com comprimentos e , respectivamente.
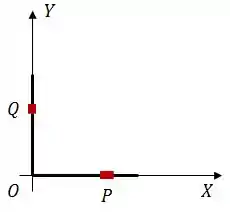
Qual é a força elétrica que o elemento em exerce sobre o elemento em ?
Passo 1
A força que o elemento em exerce sobre o elemento em é dado por:
Sabendo que , podemos reescrever esse cara como:
Vamos analisar graficamente esse cara:
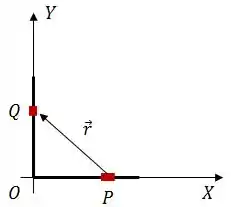
Daqui podemos tirar que:
Além disso, podemos associar as cargas e com as densidades lineares de carga:
Substituindo isso na expressão de , teremos:
Logo, a resposta certa é a letra .