Densidade de Carga, Campos Elétricos e Corpos Carregados, Potencial Elétrico
Considere um semi-anel circular, fino, de raio , situado no plano , conforme mostra a figura. Suponha que a densidade linear de carga de tal semi-anel seja dada por
onde é o tradicional ângulo polar, medido no sentido anti-horário, a partir do eixo .
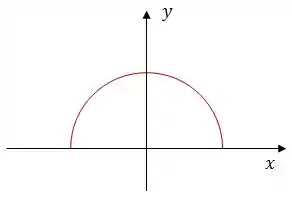
Qual é a carga elétrica total, , do semi-anel?
Calcule o campo elétrico na origem.
Calcule o potencial eletrostático em um ponto qualquer do eixo , com cota (Sabendo-se que o potencial no infinito é nulo).
Que componente(s) do campo elétrico, no mesmo ponto mencionado no item , pode(m) ser deduzida(s) a partir do resultado obtido no item anterior? Justifique e deduza-a(s).
Passo 1
Qual é a carga elétrica total, , do semi-anel?
A carga no semi-anel está associada à densidade linear de carga pela equação:
Onde , logo:
Passo 2
Calcule o campo elétrico na origem.
Vamos começar escrevendo o campo elétrico gerado por um pedaço infinitesimal do semi-anel, de carga .
Vamos analisar graficamente a situação:
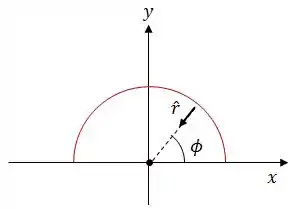
Daqui podemos tirar que:
Logo:
Antes de continuar, vamos resolver essas integrais, beleza?
Passo 3
Vamos fazer uma substituição simples:
Logo:
Substituindo de volta, teremos:
Beleza, agora vamos resolver a segunda integral:
Aqui vamos precisar lembrar da seguinte identidade trigonométrica:
Sendo assim, teremos:
Agora sim, vamos voltar ao problema.
Passo 4
Substituindo os valores, teremos:
Passo 5
Calcule o potencial eletrostático em um ponto qualquer do eixo , com cota (Sabendo-se que o potencial no infinito é nulo).
Vamos começar da mesma forma que fizemos na letra , escrevendo, agora, a expressão do potencial gerado por uma carga do semi-anel.
Onde:
Logo:
Finalmente:
Passo 6
Que componente(s) do campo elétrico, no mesmo ponto mencionado no item , pode(m) ser deduzida(s) a partir do resultado obtido no item anterior? Justifique e deduza-a(s).
De acordo com a expressão calculada no item
O potencial elétrico varia somente em função de . Assim, somente a componente em do campo elétrico pode ser calculada.
Logo:
Finalmente:
Resposta