P1 de Física 3 da UFRJ - 2016.1

Seja um capacitor ideal, com capacitância , de placas planas e paralelas, de mesma área e distância entre si, “recheado” com vácuo. Considere, agora, um novo capacitor , de placas planas e paralelas, “recheado” com um material isolante de constante dielétrica mas com distância entre as placas duas vezes maior que a do capacitor ; qual deve ser a nova área (das placas) para manter a capacitância original ? Considere, a seguir, um terceiro capacitor , de placas planas e paralelas, “recheado” com o mesmo material, mas agora com área (das placas) duas vezes maior que a do capacitor ; qual deve ser a nova distância entre as placas para manter a capacitância original ?

Considere um arame fino de comprimento , disposto ao longo do eixo simetricamente em torno do ponto . Neste arame há uma densidade linear de carga , onde é uma constante. Encontre a expressão para o potencial eletroestático num ponto genérico do plano (ou seja, plano , a uma distância do arame (supondo que, no infinito, o potencial se anule).

a)

b)

c)

d)

e) 0

Considere que os terminais de uma bateria com uma DDP conhecida estão conectados a duas placas (planas) condutoras, muito grandes, e perpendiculares ao eixo . As placas não se tocam, e têm uma distribuição superficial de cargas uniforme e estacionária. Saiba ainda que a placa de menor (maior) potencial está localizada em . Um elétron com massa e carga é lançado na região interior às placas, com uma velocidade inicial . A evolução temporal das coordenadas e do elétron dentro da região limitada pelas placas pode ser dada por:

2. ;
5. ;

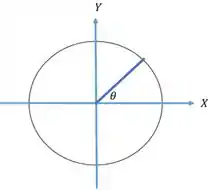
Considere um anel circular fino, de raio , com centro na origem de um sistema de coordenadas cartesianas, situado no plano . Tal anel possui uma densidade linear de carga elétrica dada por:

Onde é o usual ângulo polar medido a partir do eixo , tal como mostra a figura. Qual é o campo elétrico no centro do anel.

(a)

(b)

(c)

(d)

(e)

Uma placa condutora neutra, em equilíbrio eletroestático, quadrada, de lado e espessura , tal que , é colocada a uma distância de um plano de cargas também quadrado de lado , com densidade superficial de cargas dada por (, como mostrado na figura abaixo.

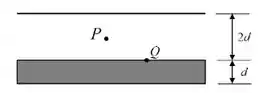
Quais são o módulo do campo elétrico no ponto localizado entre a placa e o plano, e a densidade superficial de cargas , no ponto , sobre a superfície da placa que fica mais próxima do plano?

(a)

(b)

(c)

(d)

(e)

Considere um anel circular, muito fino, de raio , com uma carga total distribuída, uniformemente (e estacionariamente) ao longo dele. O anel está no plano cartesiano (ou seja, plano ), com o eixo pelo centro do anel. Qual é o vetor campo elétrico num ponto situado no eixo

Uma partícula pontual de carga está na presença de uma esfera condutora aterrada. Verifica-se que o fluxo do campo elétrico através de uma superfície gaussiana que engloba a partícula e a esfera é , com . São feitas então as seguintes afirmativas.

1. Caso a superfície gaussiana envolvesse apenas a esfera condutora, o fluxo seria
2. A carga total induzida na esfera condutora é negativa.
3. A esfera condutora possui uma distribuição de cargas em sua superfície. Porém sua carga total é nula.
4. A carga total contida dentro da superfície gaussiana é positiva.

São verdadeiras:

1. I e II
2. I, II e IV
3. I, III e IV
4. III e IV
5. I e IV

Considere uma coroa circular com uma distribuição superficial de carga constante (estacionária e uniforme), onde . A coroa possui raio interno e raio externo e está localizada no plano , com o seu centro na origem, conforme ilustra a figura abaixo.

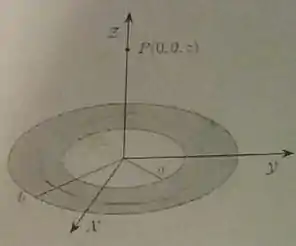
(a) Calcule o potencial eletroestático gerado por essa coroa circular no ponto , localizado no eixo , conforme ilustra a figura.

(b) Calcule o vetor campo elétrico gerado por essa coroa circular no ponto , localizado no eixo , conforme ilustra a figura.

Considere agora o limite em que o raio externo tende ao infinito, de forma que passamos a ter um plano infinito com um orifício circular de raio . A distribuição de carga contínua sendo uniforme, com densidade superficial . Para essa nova configuração, responda às perguntas a seguir.

(c) Considere que uma partícula de teste, de massa e carga , onde , tenha sido abandonada do repouso no ponto , Calcule a posição de equilíbrio da partícula no eixo . Adote a aceleração da gravidade como .

(d) Calcule a variação da energia potencial eletroestática da partícula de carga , a partir do momento em que ela foi abandonada do ponto , até passar pela origem do sistema de coordenadas.

Um corpo de dimensões desprezíveis possui massa e carga . Ele é solto do repouso do alto de uma rampa de altura . Nesta região, o campo gravitacional é constante, e há ainda um campo eletroestático presente. Sabendo-se que o corpo chega ao ponto mais baixo da rampa com velocidade , qual a diferença de potencial eletrostático entre o ponto mais baixo da rampa e o ponto de soltura do corpo?

5. Para determinarmos a diferença de potencial devemos conhecer o formato da rampa.