Considere que os terminais de uma bateria com uma DDP conhecida estão conectados a duas placas (planas) condutoras, muito grandes, e perpendiculares ao eixo . As placas não se tocam, e têm uma distribuição superficial de cargas uniforme e estacionária. Saiba ainda que a placa de menor (maior) potencial está localizada em . Um elétron com massa e carga é lançado na região interior às placas, com uma velocidade inicial . A evolução temporal das coordenadas e do elétron dentro da região limitada pelas placas pode ser dada por:
- ;
- ;
Passo 1
Segundo o enunciado a placa de cima tem potencial maior que a placa de baixo. Isso significa que podemos falar que a placa positiva é de cima e a placa negativa é de baixo.
Como o campo elétrico aponta da placa positiva para a placa negativa temos que o campo elétrico tem que apontar no sentido negativo da direção , ou seja
Como o elétron tem carga negativa, a força elétrica sobre ele vai estar na direção positiva de , pois
Como a força resultante está na direção , vamos ter um movimento uniformemente variado na direção e um movimento uniforme na direção (já que não há forças nessa direção).
O que vai acontecer é algo mais ou menos assim
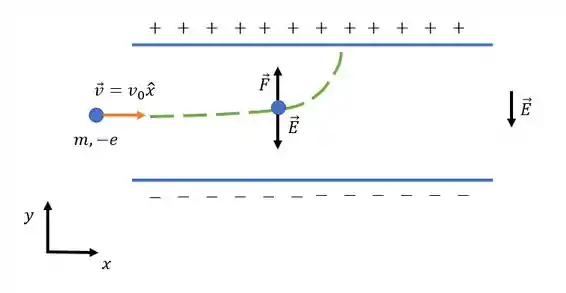
Assim já dá pra matar algumas questões 😉
Passo 2
Vamos olhar primeiro o movimento em que é mais simples.
A equação horária do movimento uniforme ficará
Simples assim 😊
Passo 3
Já sabemos a direção do campo elétrico, agora falta a sua intensidade.
Entre duas placas paralelas o campo é uniforme e se relaciona com a diferença de potencial entre as placas e a distância entre elas por
E o vetor campo elétrico é dado por
E a força sobre o elétron é dada por
Passo 4
Usando a segunda lei de Newton, a aceleração na direção é dada por
A equação horária do movimento uniformemente variado em é dada por
Como a velocidade inicial do elétron somente tem componente na direção , temos que . Assim
E pronto! Achamos as equações horárias pra e o/
Resposta
(a)