Considere um arame fino de comprimento , disposto ao longo do eixo simetricamente em torno do ponto . Neste arame há uma densidade linear de carga , onde é uma constante. Encontre a expressão para o potencial eletroestático num ponto genérico do plano (ou seja, plano , a uma distância do arame (supondo que, no infinito, o potencial se anule).
a)
b)
c)
d)
e) 0
Passo 1
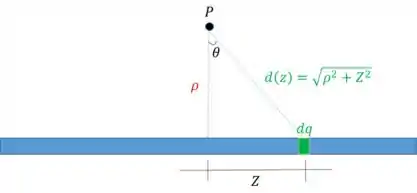
Você olha pra essa figura...bate aquela vontade de integrar quando na verdade dá pra você resolver sem fazer nenhuma conta. Na verdade, de cara, dá pra ver que a resposta é zero e o que eu pretendo fazer aqui é te convencer disso rs.
Você precisa notar algumas coisas importantes pra chegar a essa conclusão:
- A densidade de cargas é
- No lado esquerdo da barra a carga é negativa
- No lado direito da barra a carga é positiva
- E existe simetria entre o lado esquerdo e o lado direito
O potencial gerado por uma carga com distância para a direita se anula com o potencial gerado por uma carga com a mesma distância para a esquerda. Isso porque:
- Na esquerda é menor do que zero
- Coma mesma distância para a direita, temos o mesmo módulo em , só que positivo e a distância é a mesma
Logo, para cada ponto de um lado da barra, existe um ponto do outro lado que anula o potencial. Por isso, graças à simetria da questão, a resposta é zero, letra e.
Resposta
Letra e