Considere um anel circular fino, de raio , com centro na origem de um sistema de coordenadas cartesianas, situado no plano . Tal anel possui uma densidade linear de carga elétrica dada por:
Onde é o usual ângulo polar medido a partir do eixo , tal como mostra a figura. Qual é o campo elétrico no centro do anel.
(a)
(b)
(c)
(d)
(e)
Passo 1
De cara já podemos marcar a letra (a). Por que? Porque sabemos de duas coisas:
- Existe simetria nesse anel. O campo da metade superior esquerda do anel é simétrico ao campo gerado pela parte superior direita do anel.
- Por isso, a resultante do campo está no eixo e aponta para baixo. Então, a resposta tem que ser alguma coisa do tipo:
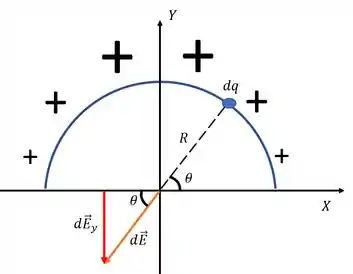
Outra forma de ver é de acordo com a figura acima. Como a distribuição de cargas está na região , vemos pela definição de que a carga é máxima em e é nula em e , ou seja, temos meio anel somente com carga positiva.
Com isso, eliminamos as letras (b), (c), (d) e (e).
Passo 2
Mas vamos resolver fingindo que a questão não é de múltipla escolha (mas na prova, tenta ser malandro, olha o tempo que você economiza...)
Encontrar o componente infinitesimal de carga.
O infinitésimo de arco é dado por
Assim
Passo 3
Note, pela simetria do problema, que o campo elétrico aponta para baixo, na posição vertical. Isso porque somente existe carga na metade de cima do anel
Além disso, a carga na parte esquerda é simétrica à carga na parte direita pois
Assim:
Passo 4
O módulo da componente infinitesimal de campo é dada por
Passo 5
Agora basta integrar a componente infinitesimal de campo:
Lembrando que:
E
Subtraindo as duas equações
A nossa integralzinha fica
E o campo elétrico fica
Passo 6
Já determinamos pela simetria que o campo tem que estar na direção , assim
Resposta
Letra (a)