Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 2212345678910111213141516171819202123242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

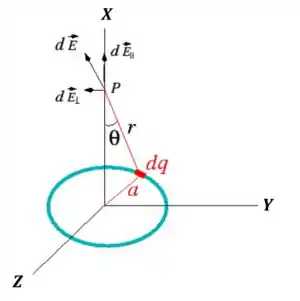
Considere um anel circular, muito fino, de raio a , com uma carga total Q distribuída, uniformemente (e estacionariamente) ao longo dele. O anel está no plano cartesiano x = 0 (ou seja, plano Y Z ), com o eixo X pelo centro do anel. Qual é o vetor campo elétrico num ponto P = ( x , 0,0 ) situado no eixo X ? K 0 = 1 4 . π . ϵ 0

  1. k 0 . Q x a 2 + x 2 3 2 . x ^
  2. - k 0 . Q x a 2 + x 2 3 2 . x ^
  3. k 0 . Q x 2 . x ^
  4. - k 0 . Q x 2 . x ^
  5. k 0 . Q x a 2 + x 2 3 2 . ( x ^ + y ^ + z ^ )
  6. - k 0 . Q x a 2 + x 2 3 2 . ( x ^ + y ^ + z ^ )

Passo 1

Calcular r : x 2 + a 2 = r 2 → r = x 2 + a 2

Passo 2

Determinar a componente infinitesimal de campo d E :

d E = K 0 . d q r 2 = K 0 . d q x 2 + a 2

Passo 3

Notar, pela simetria do problema, que a resultante do campo elétrico se encontra na direção do eixo do anel. Logo, todas as componentes que se encontram no plano do anel se anulam:

E R E S U L T A N T E = E | | = E X

E Y = E Z = 0 = E ⊥

Então, precisamos projetar d E na direção certa, na direção X ;

Passo 4

Substituir e calcular a componente E X

d E X = d E . cos ⁡ θ = d E . x r = K 0 . d q x 2 + a 2 .   x x 2 + a 2 = K 0 . d q . x x 2 + a 2 3 2

Passo 5

Integrar e achar o valor do campo resultante

E = ∫ d E x = ∫ K 0 . d q . x x 2 + a 2 3 2 = K 0 . x . ∫ d q x 2 + a 2 3 2 = K 0 . Q . x x 2 + a 2 3 2

Esse campo atua na direção x ^ , em seu sentido positivo. Por isso, já poderíamos, desde o início, ter eliminado as letras (b), (d), (e) e (f) :)

Resposta

Letra (A)

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri