Uma placa condutora neutra, em equilíbrio eletroestático, quadrada, de lado e espessura , tal que , é colocada a uma distância de um plano de cargas também quadrado de lado , com densidade superficial de cargas dada por (, como mostrado na figura abaixo.
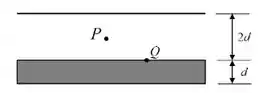
Quais são o módulo do campo elétrico no ponto localizado entre a placa e o plano, e a densidade superficial de cargas , no ponto , sobre a superfície da placa que fica mais próxima do plano?
(a)
(b)
(c)
(d)
(e)
Passo 1
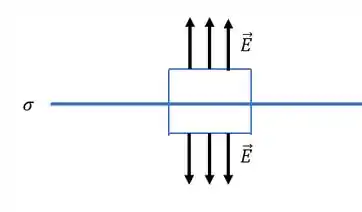
Primeiro vamos lembrar como se calcula o campo elétrico produzido pela placa de cima.
Primeiro temos que construir uma gaussiana que contenha o plano, com área da base . O campo elétrico, por simetria, tem que ser perpendicular a essa área e o fluxo do campo elétrico através gaussiana.
O fator de aparece por que temos duas tampas de área onde há fluxo de campo elétrico.
Pela lei de Gauss esse fluxo de campo elétrico é dado por
Onde é a carga total dentro da nossa superfície gaussiana. Para calcular essa carga basta multiplica a área da base dessa superfície pela densidade de carga da placa, .
Assim, temos
E esse campo elétrico aponta para fora do plano.
Passo 2
Agora, vamos lá. Se eu pego esse plano carregado e trago perto de uma superfície condutora, o que você espera? Uma indução de cargas na superfície, certo?
Se a placa tem uma densidade de carga , é natural pensar que as cargas induzidas na parte superior do condutor tenham carga de sinal contrário.
Então, digamos, uma densidade de cargas seja induzida na superfície superior do nosso condutor. Como esse condutor é neutro, então teríamos que ter uma densidade de carga na superfície inferior, correto?
A distribuição de cargas ficaria algo mais ou menos assim

Beleza? Agora já fizemos o mais difícil da questão! Agora vamo lá!
Passo 3
Cada uma das superfícies do condutor atuará como uma placa carregada. Já vimos como é o campo de uma placa carregada, né? A intensidade do campo elétrico produzido por cada uma dessas superfícies com densidade de carga será
Show! Agora vamos apontar o campo produzido por cada uma das superfícies
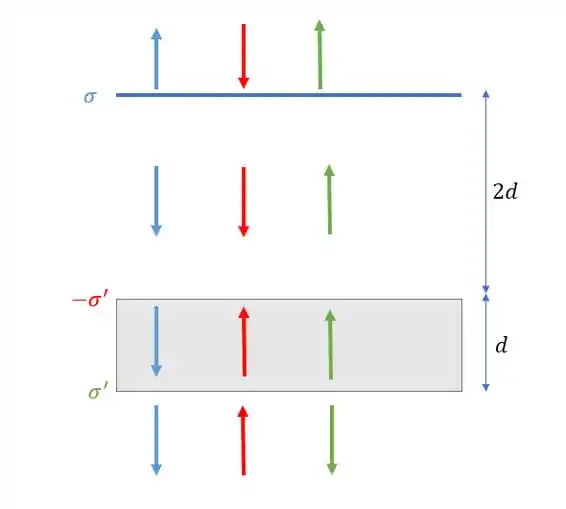
Tá, ok. A gente apontou um montão de campo.... e agora o que você faz com isso?
Agora tem que lembrar de um detalhe super mega importante pra caramba!
O campo elétrico dentro de um condutor é nulo!
Isso significa que a soma dos campos que vimos dentro do condutor é nula. Pela figura, vemos que
E estamos prontos pra responder umas das perguntas!
A densidade de cargas no ponto é dada por
Show!
Passo 4
Agora só basta calcular o campo no ponto . Tomando como positiva a direção para cima, pela figura vemos que o campo no ponto é dado por
Ou seja, o módulo do campo resultante no ponto , será
Resposta
Letra (A)