P2 de Física 3 da USP - 2011

Considere duas cascas cilíndricas condutoras coaxiais sendo que a casca interior possui raio e a exterior, raio . As cascas cilíndricas possuem comprimento . O espaço entre as cascas é preenchido uniformemente com um material cuja resistividade é . Entre os duas cascas é aplicada uma diferença de potencial tal que a corrente medida no dispositivo é .

As respostas dos itens abaixo deverão ser dadas em função apenas dos dados do problema que são , , , , e .

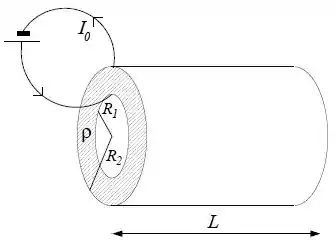
Calcule o vetor densidade de corrente a uma distância do eixo dos cilindros.

Determine o vetor campo elétrico entre os cilindros.

Usando o campo elétrico obtido em , calcule a diferença de potencial entre os cilindros.

Calcule a resistência do sistema.

Uma partícula carregada com carga e massa é acelerada paralelamente ao eixo , no sentido de crescente, a partir do repouso, por uma diferença de potencial .

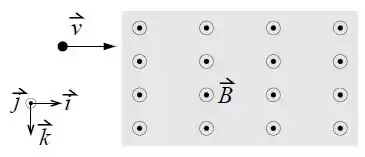
Determine o vetor velocidade final da partícula após a aceleração do potencial .

A partícula carregada adentra a seguir numa região de campo magnético uniforme . Determine o vetor força magnética que atua sobre a partícula em função de , , e .

Faça um esquema do movimento dessa partícula na região de campo . Calcule o raio da trajetória na região com campo magnético e o tempo gasto nesta região.

Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.

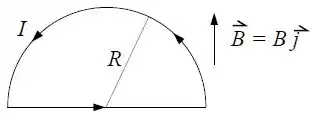
Determine o vetor torque exercido por sobre o circuito.

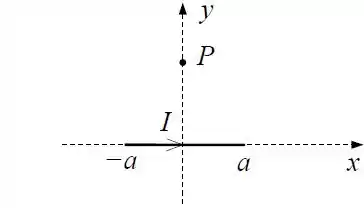
Considere um fio de comprimento por onde passa uma corrente colocado ao longo do eixo , conforme a figura.

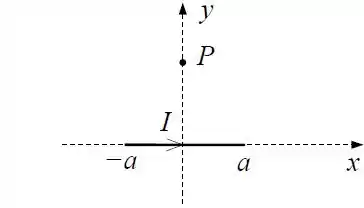
Usando a lei de Ampère, calcule o campo magnético em para o fio infinito do item .

Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.

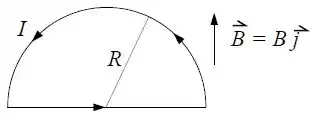
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.

Determine a força magnética total (vetor) sobre a parte curva do condutor.

Considere um fio de comprimento por onde passa uma corrente colocado ao longo do eixo , conforme a figura.

Usando a lei de Biot-Savart, calcule o campo magnético num ponto do eixo .

Calcule o campo magnético no limite em que .