Potencial Elétrico, Corrente e Resistores
Considere duas cascas cilíndricas condutoras coaxiais sendo que a casca interior possui raio e a exterior, raio . As cascas cilíndricas possuem comprimento . O espaço entre as cascas é preenchido uniformemente com um material cuja resistividade é . Entre os duas cascas é aplicada uma diferença de potencial tal que a corrente medida no dispositivo é .
As respostas dos itens abaixo deverão ser dadas em função apenas dos dados do problema que são , , , , e .
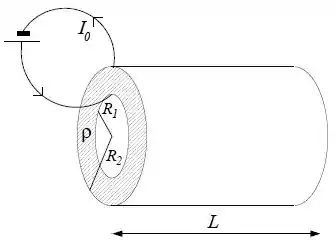
Calcule o vetor densidade de corrente a uma distância do eixo dos cilindros.
Determine o vetor campo elétrico entre os cilindros.
Usando o campo elétrico obtido em , calcule a diferença de potencial entre os cilindros.
Calcule a resistência do sistema.
Passo 1
Calcule o vetor densidade de corrente a uma distância do eixo dos cilindros.
A densidade de corrente está associada com a corrente através da relação:
Onde é a área por onde a corrente passa.
Analisando a figura, podemos ver que a corrente flui da superfície interna do cilindro para a superfície externa. Assim, será a área lateral do cilindro de raio , dada por .
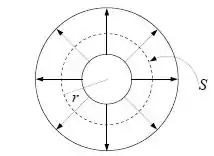
Portanto:
Novamente, como a corrente flui da superfície interna para a superfície externa, o vetor densidade de corrente terá direção radial, e o sentido será de dentro para fora. Assim:
Passo 2
Determine o vetor campo elétrico entre os cilindros.
O vetor campo elétrico e o vetor densidade de corrente estão associados por:
Agora ficou fácil...
Passo 3
Usando o campo elétrico obtido em , calcule a diferença de potencial entre os cilindros.
Por definição, a diferença de potencial é dada por:
Onde .
Substituindo os valores:
Passo 4
Calcule a resistência do sistema.
Já temos a diferença de potencial e a corrente... agora ficou tranquilo pro nosso lado:
Substituindo pela expressão que encontramos no item e por , teremos:
Finalmente:
Resposta