Uma partícula carregada com carga e massa é acelerada paralelamente ao eixo , no sentido de crescente, a partir do repouso, por uma diferença de potencial .
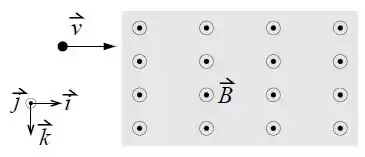
Determine o vetor velocidade final da partícula após a aceleração do potencial .
A partícula carregada adentra a seguir numa região de campo magnético uniforme . Determine o vetor força magnética que atua sobre a partícula em função de , , e .
Faça um esquema do movimento dessa partícula na região de campo . Calcule o raio da trajetória na região com campo magnético e o tempo gasto nesta região.
Passo 1
Determine o vetor velocidade final da partícula após a aceleração do potencial .
No instante antes de entrar em movimento, a energia da partícula é . Quando ela começa a ser acelerada, essa energia vai se transformando em energia cinética.
No final das contas, toda a energia da partícula é convertida em energia cinética, logo:
Como a partícula está se movendo no sentido , o vetor velocidade final será:
Passo 2
A partícula carregada adentra a seguir numa região de campo magnético uniforme . Determine o vetor força magnética que atua sobre a partícula em função de , , e .
Por definição, a força magnética sobre uma partícula é dada por:
Substituindo pela expressão que encontramos na letra , teremos:
Só pra dar uma organizada nesse cara, podemos pegar esse e jogar para dentro da raíz.
Finalmente:
Passo 3
Faça um esquema do movimento dessa partícula na região de campo . Calcule o raio da trajetória na região com campo magnético e o tempo gasto nesta região.
Como a força magnética estará sempre perpendicular à velocidade e ao campo magnético , a partícula vai percorrer uma trajetória circular.
Essa trajetória vai ter essa cara:
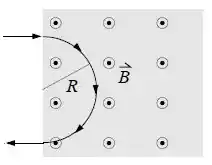
Passo 4
Para calcular o raio da trajetória circular, basta ver que a força magnética será, também a força centrípeta que manterá a partícula na trajetória circular. Logo:
Pra finalizar, basta substituir a expressão de que já tínhamos calculado no item .
Organizando esse cara:
Passo 5
Como a partícula permanece com velocidade constante nessa região, pra calcularmos o tempo gasto na região com o campo elétrico, basta fazer:
Pra finalizar, temos apenas que substituir as expressões de e que encontramos anteriormente:
Finalmente:
Resposta