Considere um fio de comprimento por onde passa uma corrente colocado ao longo do eixo , conforme a figura.
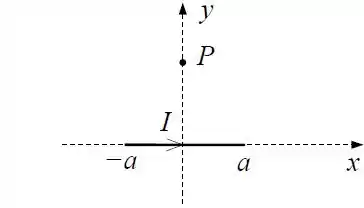
Usando a lei de Ampère, calcule o campo magnético em para o fio infinito do item .
Passo 1
Usando a lei de Ampère, calcule o campo magnético em para o fio infinito do item .
A Lei de Ampère é dada por:
Podemos dar uma simplificada nessa expressão, que pode ser reescrita por:
Essa integral nos dará o tamanho da nossa amperiana, que se trata da circunferência de raio . Além disso, a corrente que passa pela amperiana será . Logo:
A direção e o sentido vetor campo magnético são determinados através da regra da mão direita. Como a corrente está fluindo da esquerda para a direita, no ponto o campo estará saindo da página.
Portanto:
Resposta